Page 526 - Acquisition and Processing of Marine Seismic Data

11.5 REVERSE TIME MIGRATION 517

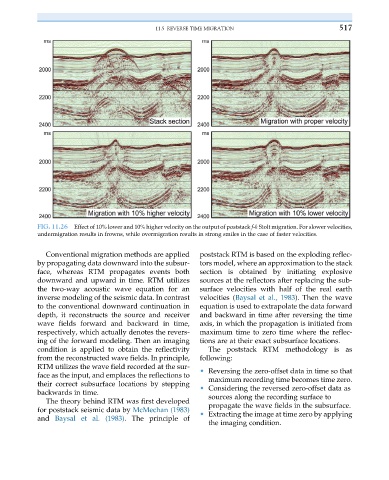
FIG. 11.26 Effect of 10% lower and 10% higher velocity on the output of poststack f-k Stolt migration. For slower velocities,
undermigration results in frowns, while overmigration results in strong smiles in the case of faster velocities.

Conventional migration methods are applied poststack RTM is based on the exploding reflec-
by propagating data downward into the subsur- tors model, where an approximation to the stack
face, whereas RTM propagates events both section is obtained by initiating explosive
downward and upward in time. RTM utilizes sources at the reflectors after replacing the sub-
the two-way acoustic wave equation for an surface velocities with half of the real earth
inverse modeling of the seismic data. In contrast velocities (Baysal et al., 1983). Then the wave
to the conventional downward continuation in equation is used to extrapolate the data forward
depth, it reconstructs the source and receiver and backward in time after reversing the time
wave fields forward and backward in time, axis, in which the propagation is initiated from
respectively, which actually denotes the revers- maximum time to zero time where the reflec-
ing of the forward modeling. Then an imaging tions are at their exact subsurface locations.
condition is applied to obtain the reflectivity The poststack RTM methodology is as
from the reconstructed wave fields. In principle, following:
RTM utilizes the wave field recorded at the sur-
• Reversing the zero-offset data in time so that
face as the input, and emplaces the reflections to
maximum recording time becomes time zero.
their correct subsurface locations by stepping
• Considering the reversed zero-offset data as
backwards in time.
sources along the recording surface to
The theory behind RTM was first developed
propagate the wave fields in the subsurface.
for poststack seismic data by McMechan (1983)
• Extracting the image at time zero by applying
and Baysal et al. (1983). The principle of
the imaging condition.