Page 62 - Adsorbents fundamentals and applications

SIMPLE CRITERIA FOR SORBENT SELECTION 47

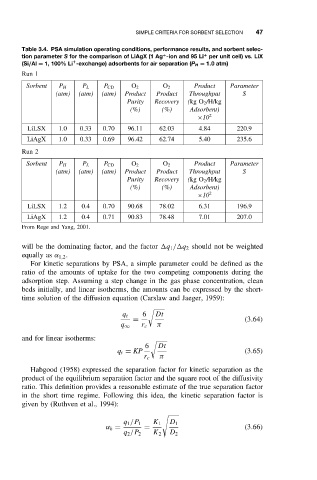
Table 3.4. PSA simulation operating conditions, performance results, and sorbent selec-
+
tion parameter S for the comparison of LiAgX (1 Ag -ion and 95 Li per unit cell) vs. LiX
+
+
(Si/Al = 1, 100% Li -exchange) adsorbents for air separation (P H = 1.0atm)
Run 1
Sorbent P H P L P CD O 2 O 2 Product Parameter
(atm) (atm) (atm) Product Product Throughput S
Purity Recovery (kg O 2 /H/kg
(%) (%) Adsorbent)
×10 2
LiLSX 1.0 0.33 0.70 96.11 62.03 4.84 220.9
LiAgX 1.0 0.33 0.69 96.42 62.74 5.40 235.6
Run 2
Sorbent P H P L P CD O 2 O 2 Product Parameter
(atm) (atm) (atm) Product Product Throughput S
Purity Recovery (kg O 2 /H/kg
(%) (%) Adsorbent)
×10 2
LiLSX 1.2 0.4 0.70 90.68 78.02 6.31 196.9
LiAgX 1.2 0.4 0.71 90.83 78.48 7.01 207.0
From Rege and Yang, 2001.

will be the dominating factor, and the factor q 1 / q 2 should not be weighted
equally as α 1,2 .
For kinetic separations by PSA, a simple parameter could be defined as the
ratio of the amounts of uptake for the two competing components during the
adsorption step. Assuming a step change in the gas phase concentration, clean
beds initially, and linear isotherms, the amounts can be expressed by the short-
time solution of the diffusion equation (Carslaw and Jaeger, 1959):

6 Dt
q t
= (3.64)
q ∞ r c π
and for linear isotherms:

6 Dt
q t = KP (3.65)
r c π
Habgood (1958) expressed the separation factor for kinetic separation as the
product of the equilibrium separation factor and the square root of the diffusivity
ratio. This definition provides a reasonable estimate of the true separation factor
in the short time regime. Following this idea, the kinetic separation factor is
given by (Ruthven et al., 1994):

q 1 /P 1 K 1 D 1
α k = = (3.66)
q 2 /P 2 K 2 D 2