Page 26 - Advanced_Engineering_Mathematics o'neil

6 CHAPTER 1 First-Order Differential Equations

2

x
0.4 0.8 1.2 1.6 2
0 x

–2

–4

–6
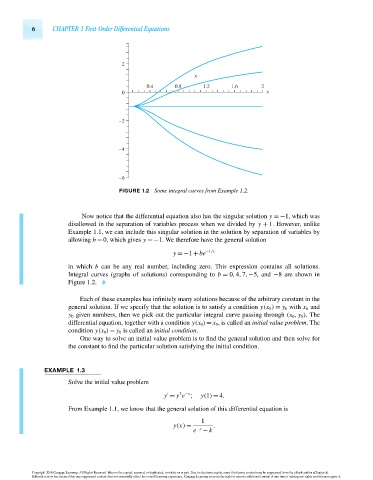
FIGURE 1.2 Some integral curves from Example 1.2.

Now notice that the differential equation also has the singular solution y =−1, which was
disallowed in the separation of variables process when we divided by y + 1. However, unlike
Example 1.1, we can include this singular solution in the solution by separation of variables by
allowing b = 0, which gives y =−1. We therefore have the general solution
y =−1 + be −1/x

in which b can be any real number, including zero. This expression contains all solutions.
Integral curves (graphs of solutions) corresponding to b = 0,4,7,−5, and −8 are shown in
Figure 1.2.

Each of these examples has infinitely many solutions because of the arbitrary constant in the
general solution. If we specify that the solution is to satisfy a condition y(x 0 ) = y 0 with x 0 and
y 0 given numbers, then we pick out the particular integral curve passing through (x 0 , y 0 ).The
differential equation, together with a condition y(x 0 ) = x 0 , is called an initial value problem.The
condition y(x 0 ) = y 0 is called an initial condition.
One way to solve an initial value problem is to find the general solution and then solve for
the constant to find the particular solution satisfying the initial condition.

EXAMPLE 1.3
Solve the initial value problem
2 −x
y = y e ; y(1) = 4.
From Example 1.1, we know that the general solution of this differential equation is
1
y(x) = .
e −x − k

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:9 THM/NEIL Page-6 27410_01_ch01_p01-42