Page 573 - Advanced_Engineering_Mathematics o'neil

15.3 Bessel Functions 553

0.3

0.2

0.1

0
0 5 10 15 20 25
x
–0.1

–0.2

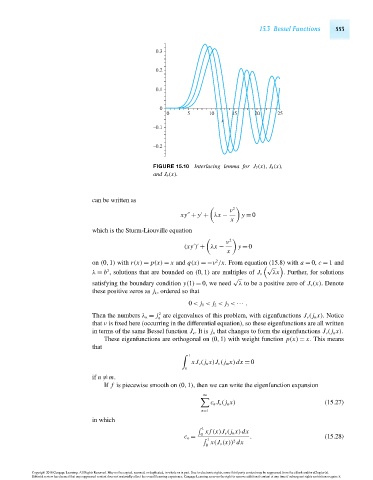
FIGURE 15.10 Interlacing lemma for J 7 (x), J 8 (x),
and J 9 (x).

can be written as

2
ν

xy + y + λx − y = 0
x
which is the Sturm-Liouville equation

2
ν

(xy ) + λx − y = 0
x
2
on (0,1) with r(x) = p(x) = x and q(x) =−ν /x. From equation (15.8) with a = 0, c = 1 and
√

2
λ = b , solutions that are bounded on (0,1) are multiples of J ν λx . Further, for solutions
√
satisfying the boundary condition y(1) = 0, we need λ to be a positive zero of J ν (x). Denote
these positive zeros as j k , ordered so that
0 < j 1 < j 2 < j 3 < ··· .
2
Then the numbers λ n = j are eigenvalues of this problem, with eigenfunctions J ν ( j n x). Notice
n
that ν is fixed here (occurring in the differential equation), so these eigenfunctions are all written
in terms of the same Bessel function J ν .Itis j n that changes to form the eigenfunctions J ν ( j n x).
These eigenfunctions are orthogonal on (0,1) with weight function p(x) = x. This means
that
1
xJ ν ( j n x)J ν ( j m x)dx = 0
0
if n = m.
If f is piecewise smooth on (0,1), then we can write the eigenfunction expansion
∞

c n J ν ( j n x) (15.27)
n=1
in which
1
0 xf (x)J ν ( j n x)dx
c n = . (15.28)
1
2
x(J ν (x)) dx
0
Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 15:20 THM/NEIL Page-553 27410_15_ch15_p505-562