Page 153 - Advanced Gas Turbine Cycles

1 24 Advanced gas turbine cycles

Turbine inlet
- 0.36 temperature
1400 "C
OY
- 0.34
I
2 0.32 -Turbine inlet
Q temperature
c
$ 0.30 1400 'C
E a
0
ZI 1300 "C
c
.- 1400 'C Y
0)
$ Y 1200 "C
0
- - 3
2 0 1100°C
Q) 0
6 Q
u
1000 "C 1000 "C
10 15 20 30 10 15 20 30
Pressure ratio Pressure ratio
Gas turbine plant Combined plant
(non-reheat)
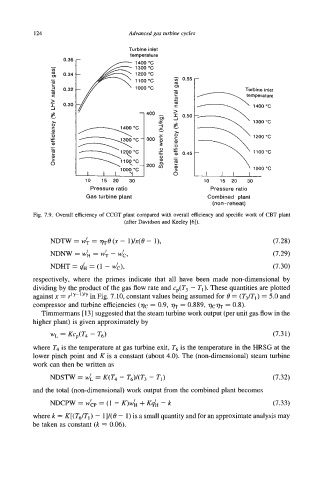
Fig. 7.9. Overall efficiency of CCGT plant compared with overall efficiency and specific work of CBT plant
(after Davidson and Keeley [6]).

NDTW = W; = we(n - i)/~(e - I), (7.28)
I
NDNW = W'H = W'T - wc, (7.29)
NDHT = dH = (1 - Wk), (7.30)
respectively, where the primes indicate that all have been made non-dimensional by
dividing by the product of the gas flow rate and c (T - Tl). These quantities are plotted
p.
against n = r-(y-')'y in Fig. 7.10, constant values being assumed for 8 = (T3/Tl) = 5.0 and
compressor and turbine efficiencies (qc = 0.9, = 0.889, ww = 0.8).
Timmermans [ 131 suggested that the steam turbine work output (per unit gas flow in the
higher plant) is given approximately by
WL = KcP(T4 - T6) (7.31)
where T4 is the temperature at gas turbine exit, T6 is the temperature in the HRSG at the
lower pinch point and K is a constant (about 4.0). The (non-dimensional) steam turbine
work can then be written as

NDsTW = dL = K(T4 - T6)/(T3 - TI) (7.32)
and the total (non-dimensional) work output from the combined plant becomes
NDCPW = wbp = (1 - K)wh + Kqh - k (7.33)
where k = K[(T6/T,) - 1]/(8 - 1) is a small quantity and for an approximate analysis may
be taken as constant (k = 0.06).