Page 453 - Advanced Linear Algebra

Affine Geometry 437

It is not hard to see that is a well-defined group homomorphism from aff²= ³

onto B²= ³ , with kernel trans ²= ³ . Hence, trans ²= ³ is a normal subgroup of
aff²= ³ and
aff²= ³
š²= ³
B
trans²= ³
Projective Geometry

)
(
If dim²= ³ ~ , the join affine hull of any two distinct points in is a line. On
=
the other hand, it is not the case that the intersection of any two lines is a point,
since the lines may be parallel. Thus, there is a certain asymmetry between the
concepts of points and lines in = . This asymmetry can be removed by
constructing the projective plane . Our plan here is to very briefly describe one
possible construction of projective geometries of all dimensions.
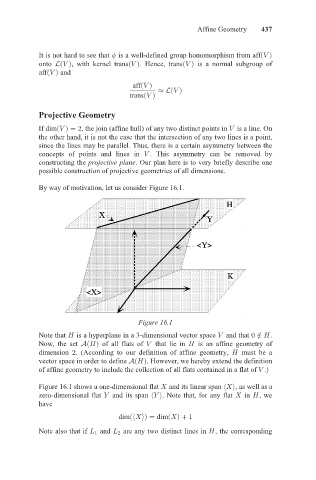
By way of motivation, let us consider Figure 16.1.

Figure 16.1

Note that is a hyperplane in a 3-dimensional vector space and that ¤ = / .
/
Now, the set 7²/³ of all flats of = that lie in / is an affine geometry of
dimension . According to our definition of affine geometry, / ( must be a

vector space in order to define 7²/³ . However, we hereby extend the definition
of affine geometry to include the collection of all flats contained in a flat of .=³
?
Figure 16.1 shows a one-dimensional flat and its linear span ? º » , as well as a
zero-dimensional flat and its span º @ » . Note that, for any flat in / ? , we
@
have
dim²º?»³ ~ dim²?³ b
Note also that if 3 and 3 are any two distinct lines in / , the corresponding