Page 131 - Advanced engineering mathematics

3.6 Solution of Systems 111

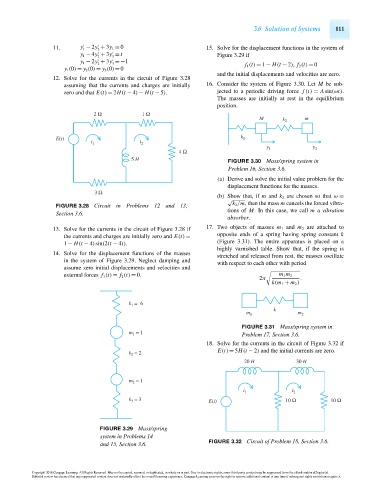
11. y − 2y + 3y 1 = 0 15. Solve for the displacement functions in the system of
2
1
y 1 − 4y + 3y = t Figure 3.29 if

2 3

y 1 − 2y + 3y =−1

2 3 f 1 (t) = 1 − H(t − 2), f 2 (t) = 0
y 1 (0) = y 2 (0) = y 3 (0)= 0
and the initial displacements and velocities are zero.
12. Solve for the currents in the circuit of Figure 3.28
assuming that the currents and charges are initially 16. Consider the system of Figure 3.30. Let M be sub-
zero and that E(t) = 2H(t − 4) − H(t − 5). jected to a periodic driving force f (t) = A sin(ωt).
The masses are initially at rest in the equilibrium
position.
2 Ω 1 Ω
M k m
2
E(t) k 1
i 1 i 2
y 1 y 2
4 Ω
5 H FIGURE 3.30 Mass/spring system in
Problem 16, Section 3.6.
(a) Derive and solve the initial value problem for the
displacement functions for the masses.
3 Ω
(b) Show that, if m and k 2 are chosen so that ω =
√
FIGURE 3.28 Circuit in Problems 12 and 13, k 2 /m, then the mass m cancels the forced vibra-
tions of M. In this case, we call m a vibration
Section 3.6.
absorber.
13. Solve for the currents in the circuit of Figure 3.28 if 17. Two objects of masses m 1 and m 2 are attached to
opposite ends of a spring having spring constant k
the currents and charges are initially zero and E(t) =
1 − H(t − 4)sin(2(t − 4)). (Figure 3.31). The entire apparatus is placed on a
highly varnished table. Show that, if the spring is
14. Solve for the displacement functions of the masses
stretched and released from rest, the masses oscillate
in the system of Figure 3.29. Neglect damping and
with respect to each other with period
assume zero initial displacements and velocities and

external forces f 1 (t) = f 2 (t) = 0. m 1 m 2
2π .
k(m 1 + m 2 )
k = 6
1
k
m 1 m 2
FIGURE 3.31 Mass/spring system in
m 1 = 1 Problem 17, Section 3.6.
18. Solve for the currents in the circuit of Figure 3.32 if
E(t) = 5H(t − 2) and the initial currents are zero.
= 2
k 2
20 H 30 H
= 1
m 2
i 1 i 2
k = 3 E(t) 10 Ω 10 Ω
3

FIGURE 3.29 Mass/spring
system in Problems 14
FIGURE 3.32 Circuit of Problem 18, Section 3.6.
and 15, Section 3.6.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:14 THM/NEIL Page-111 27410_03_ch03_p77-120