Page 178 - Advanced engineering mathematics

158 CHAPTER 6 Vectors and Vector Spaces

Then
−2(x + 6) + 4(y − 1) + (z − 1) = 0,
or

−2x + 4y + z = 17.
This is the equation of .

Following this reasoning in general, the equation of a plane containing a point P 0 :(x 0 , y 0 , z 0 )
and having a normal vector N = ai + bj + ck is

N ·[(x − x 0 )i + (y − y 0 )j + (z − z 0 )k]= 0
or
a(x − x 0 ) + b(y − y 0 ) + c(z − z 0 ) = 0. (6.2)
It is also sometimes convenient to notice that the vector ai + bj + ck is always a normal
vector to a plane ax + by + cz = d, for any d. Changing the value of d moves the plane in 3-
space but does not change its orientation with respect to the axes, so the normal vector remains
the same and is determined by the coefficients a, b, and c only.
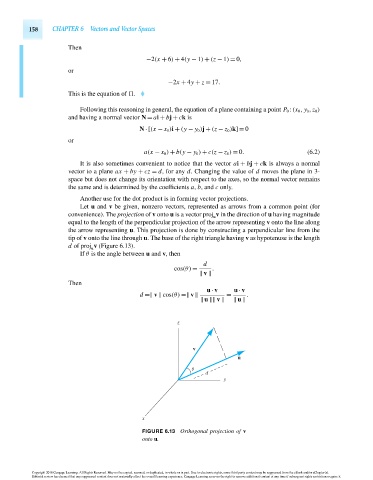
Another use for the dot product is in forming vector projections.
Let u and v be given, nonzero vectors, represented as arrows from a common point (for
convenience). The projection of v onto u is a vector proj v in the direction of u having magnitude
u
equal to the length of the perpendicular projection of the arrow representing v onto the line along
the arrow representing u. This projection is done by constructing a perpendicular line from the
tip of v onto the line through u. The base of the right triangle having v as hypotenuse is the length
d of proj v (Figure 6.13).
u
If θ is the angle between u and v, then
d
cos(θ) = .
v
Then
u · v u · v
d = v cos(θ) = v = .
u v u

z

v
u
θ
d
y

x
FIGURE 6.13 Orthogonal projection of v
onto u.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:21 THM/NEIL Page-158 27410_06_ch06_p145-186