Page 206 - Advanced engineering mathematics

186 CHAPTER 6 Vectors and Vector Spaces

2.5 2.5

2 2

1.5 1.5

1 1

0.5 0.5

–1 –0.5 0 0.5 1 –1 –0.5 0 0.5 1
x x

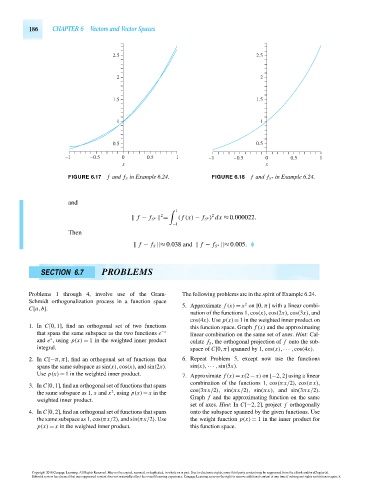
FIGURE 6.17 f and f S in Example 6.24. FIGURE 6.18 f and f S ∗ in Example 6.24.

and
1
2 2
f − f S ∗ = ( f (x) − f S ∗) dx ≈ 0.000022.
−1
Then
f − f S ≈ 0.038 and f − f S ∗ ≈ 0.005.

SECTION 6.7 PROBLEMS

Problems 1 through 4, involve use of the Gram- The following problems are in the spirit of Example 6.24.
Schmidt orthogonalization process in a function space
2
5. Approximate f (x) = x on [0,π] with a linear combi-
C[a,b].
nation of the functions 1, cos(x),cos(2x),cos(3x),and
cos(4x).Use p(x)=1 in the weighted inner product on
1. In C[0,1], find an orthogonal set of two functions this function space. Graph f (x) and the approximating
that spans the same subspace as the two functions e −x linear combination on the same set of axes. Hint:Cal-
x
and e ,using p(x) = 1 in the weighted inner product culate f S , the orthogonal projection of f onto the sub-
integral. space of C[0,π] spanned by 1, cos(x),··· ,cos(4x).
2. In C[−π,π], find an orthogonal set of functions that 6. Repeat Problem 5, except now use the functions
spans the same subspace as sin(x),cos(x),and sin(2x). sin(x),··· ,sin(5x).
Use p(x) = 1 in the weighted inner product. 7. Approximate f (x)= x(2 − x) on [−2,2] using a linear
combination of the functions 1, cos(πx/2),cos(πx),
3. In C[0,1], find an orthogonal set of functions that spans
2
the same subspace as 1, x and x ,using p(x) = x in the cos(3πx/2),sin(πx/2),sin(πx),and sin(3πx/2).
Graph f and the approximating function on the same
weighted inner product.
set of axes. Hint:In C[−2,2],project f orthogonally
4. In C[0,2], find an orthogonal set of functions that spans onto the subspace spanned by the given functions. Use
the same subspace as 1,cos(πx/2),and sin(πx/2).Use the weight function p(x) = 1 in the inner product for
p(x) = x in the weighted inner product. this function space.

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:21 THM/NEIL Page-186 27410_06_ch06_p145-186