Page 455 - Advanced engineering mathematics

13.2 The Fourier Series of a Function 435

2.5

2

1.5

1

0.5

–1 –0.5 0 0.5 1
x
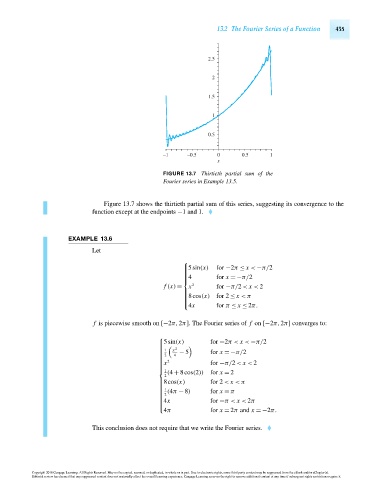
FIGURE 13.7 Thirtieth partial sum of the
Fourier series in Example 13.5.

Figure 13.7 shows the thirtieth partial sum of this series, suggesting its convergence to the
function except at the endpoints −1 and 1.

EXAMPLE 13.6

Let

⎧
⎪5sin(x) for −2π ≤ x < −π/2
⎪
⎪
⎪
⎪4 for x =−π/2
⎪
⎨
f (x) = x 2 for −π/2 < x < 2
⎪
⎪8cos(x) for 2 ≤ x <π
⎪
⎪
⎪
⎪
4x for π ≤ x ≤ 2π.
⎩
f is piecewise smooth on [−2π,2π]. The Fourier series of f on [−2π,2π] converges to:
⎧
⎪5sin(x) for −2π< x < −π/2

⎪
⎪
⎪ 1 π 2
⎪ − 5 for x =−π/2
⎪ 2 4
⎪
⎪
⎪ 2 for −π/2 < x < 2
⎪x
⎪
⎪
⎪
⎨ 1 (4 + 8cos(2)) for x = 2
2
⎪8cos(x) for 2 < x <π
⎪
⎪
⎪
⎪ 1
⎪ (4π − 8) for x = π
⎪
⎪ 2
⎪
⎪ 4x for −π< x < 2π
⎪
⎪
⎪
4π for x = 2π and x =−2π.
⎩
This conclusion does not require that we write the Fourier series.
Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.
October 14, 2010 14:57 THM/NEIL Page-435 27410_13_ch13_p425-464