Page 458 - Advanced engineering mathematics

438 CHAPTER 13 Fourier Series

1

0.8

0.6

0.4

0.2

0
–1 –0.5 0 0.5 1
x
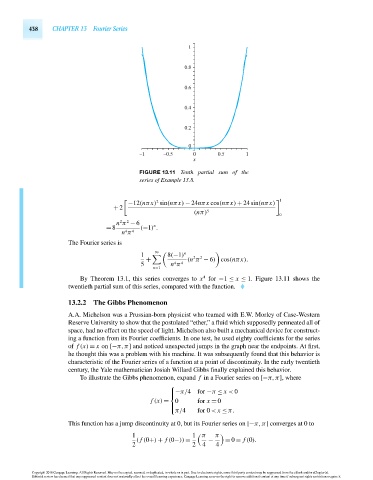
FIGURE 13.11 Tenth partial sum of the
series of Example 13.8.

1
2
−12(nπx) sin(nπx) − 24nπx cos(nπx) + 24sin(nπx)
+ 2
(nπ) 5
0
2
2
n π − 6 n
=8 (−1) .
4
n π 4
The Fourier series is
1 8(−1) n
∞
2
2
+ (n π − 6) cos(nπx).
5 n π 4
4
n=1
4
By Theorem 13.1, this series converges to x for −1 ≤ x ≤ 1. Figure 13.11 shows the
twentieth partial sum of this series, compared with the function.
13.2.2 The Gibbs Phenomenon
A.A. Michelson was a Prussian-born physicist who teamed with E.W. Morley of Case-Western
Reserve University to show that the postulated “ether,” a fluid which supposedly permeated all of
space, had no effect on the speed of light. Michelson also built a mechanical device for construct-
ing a function from its Fourier coefficients. In one test, he used eighty coefficients for the series
of f (x) = x on [−π,π] and noticed unexpected jumps in the graph near the endpoints. At first,
he thought this was a problem with his machine. It was subsequently found that this behavior is
characteristic of the Fourier series of a function at a point of discontinuity. In the early twentieth
century, the Yale mathematician Josiah Willard Gibbs finally explained this behavior.
To illustrate the Gibbs phenomenon, expand f in a Fourier series on [−π,π], where
⎧
⎪−π/4 for −π ≤ x < 0
⎨
f (x) = 0 for x = 0
⎪
π/4 for 0 < x ≤ π.
⎩
This function has a jump discontinuity at 0, but its Fourier series on [−π,π] converges at 0 to
1 1 π π

( f (0+) + f (0−)) = − = 0 = f (0).
2 2 4 4

Copyright 2010 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s).
Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.

October 14, 2010 14:57 THM/NEIL Page-438 27410_13_ch13_p425-464