Page 153 - Advanced thermodynamics for engineers

6.7 PROBLEMS 139

P6.4 Explain why the Carnot cycle overestimates the thermal efficiency achievable from an engine
producing power output. Discuss why external irreversibility reduces the effective temperature
ratio of an endoreversible engine.
Show that the thermal efficiency at maximum power output of an endoreversible engine
executing an Otto cycle is
1=2

T C
h ¼ 1
th
T H
where T H ¼ maximum temperature of the cycle and T C ¼ minimum temperature of the cycle.
P6.5 The operating processes of a spark-ignition engine can be represented by the Otto cycle, which
is internally reversible and gives a thermal efficiency of
1
h Otto ¼ 1 ;
r ðk 1Þ
where r ¼ volumetric compression ratio; k ¼ ratio of specific heats, c p /c v .
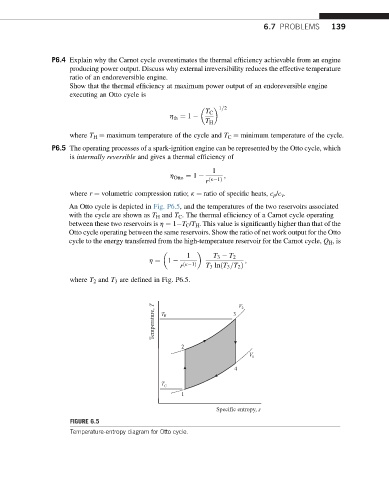
An Otto cycle is depicted in Fig. P6.5, and the temperatures of the two reservoirs associated
with the cycle are shown as T H and T C . The thermal efficiency of a Carnot cycle operating
between these two reservoirs is h ¼ 1 T C /T H . This value is significantly higher than that of the
Otto cycle operating between the same reservoirs. Show the ratio of net work output for the Otto
cycle to the energy transferred from the high-temperature reservoir for the Carnot cycle, Q H ,is

1 T 3 T 2

h ¼ 1 ;
r ðk 1Þ T 3 lnðT 3 =T 2 Þ
where T 2 and T 3 are defined in Fig. P6.5.

Temperature, T T H 3 V 2

2
V 1
4

T C
1
Specific entropy, s
FIGURE 6.5
Temperature-entropy diagram for Otto cycle.