Page 229 - Advanced thermodynamics for engineers

216 CHAPTER 10 THERMODYNAMICS OF COMBUSTION

the ‘calorimeter’ to achieve equal temperatures for the reactants and products (it is positive for some
reactions, meaning that heat has to be transferred to the calorimeter to maintain constant tempera-
tures). The value of the constant volume heat of reaction, the internal energy of reaction, (Q v ) s , can be
calculated from (Q p ) s as shown in Eqn (10.13) below, or measured using a constant volume combustion
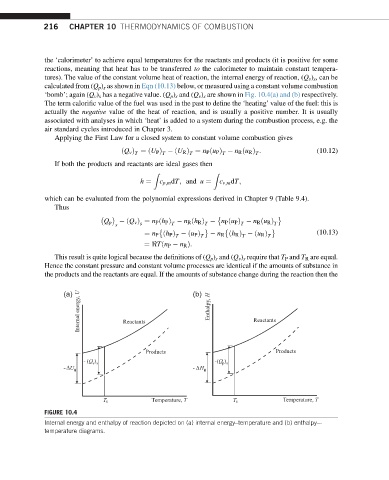
‘bomb’; again (Q v ) s has a negative value. (Q p ) s and (Q v ) s are shown in Fig. 10.4(a) and (b) respectively.
The term calorific value of the fuel was used in the past to define the ‘heating’ value of the fuel: this is
actually the negative value of the heat of reaction, and is usually a positive number. It is usually
associated with analyses in which ‘heat’ is added to a system during the combustion process, e.g. the
air standard cycles introduced in Chapter 3.
Applying the First Law for a closed system to constant volume combustion gives

ðQ v Þ ¼ðU P Þ ðU R Þ ¼ n P ðu P Þ n R ðu R Þ : (10.12)
T T T T T
If both the products and reactants are ideal gases then
Z Z
h ¼ c p;m dT; and u ¼ c v;m dT;

which can be evaluated from the polynomial expressions derived in Chapter 9 (Table 9.4).
Thus

Q p ðQ v Þ ¼ n P ðh P Þ n R ðh R Þ n P ðu P Þ n R ðu R Þ T
T
s
T
T
s

¼ n P ðh P Þ ðu P Þ n R ðh R Þ ðu R Þ (10.13)
T T T T
¼<Tðn P n R Þ:
This result is quite logical because the definitions of (Q p ) s and (Q v ) s require that T P and T R are equal.
Hence the constant pressure and constant volume processes are identical if the amounts of substance in
the products and the reactants are equal. If the amounts of substance change during the reaction then the
Internal energy, U Reactants Enthalpy, H Reactants
(a) (b)

Products Products
- (Q ) vs -(Q ) ps
Δ
Δ
- U - H
0 0

T s Temperature, T T s Temperature, T
FIGURE 10.4
Internal energy and enthalpy of reaction depicted on (a) internal energy–temperature and (b) enthalpy–-
temperature diagrams.