Page 59 - Advances in Textile Biotechnology

38 Advances in textile biotechnology

1
Concentration of enzyme in yarn, E 0.6
0.8

0.4

0.2

0
–4 –3 –2 –1
10 10 10 10 1
Fourier number, Fo
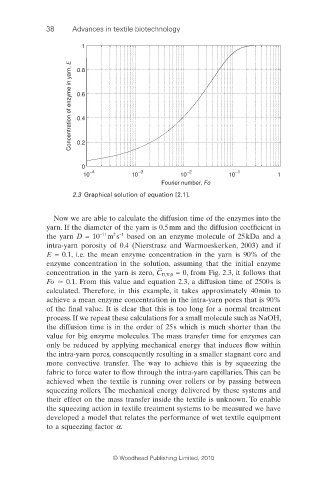
2.3 Graphical solution of equation [2.1].

Now we are able to calculate the diffusion time of the enzymes into the
yarn. If the diameter of the yarn is 0.5 mm and the diffusion coeffi cient in
2 −1
−11
the yarn D = 10 m s based on an enzyme molecule of 25 kDa and a
intra-yarn porosity of 0.4 (Nierstrasz and Warmoeskerken, 2003) and if
E = 0.1, i.e. the mean enzyme concentration in the yarn is 90% of the
enzyme concentration in the solution, assuming that the initial enzyme
concentration in the yarn is zero, C E,Y,0 = 0, from Fig. 2.3, it follows that
Fo 0.1. From this value and equation 2.3, a diffusion time of 2500 s is
calculated. Therefore, in this example, it takes approximately 40 min to
achieve a mean enzyme concentration in the intra-yarn pores that is 90%

of the final value. It is clear that this is too long for a normal treatment
process. If we repeat these calculations for a small molecule such as NaOH,
the diffusion time is in the order of 25 s which is much shorter than the
value for big enzyme molecules. The mass transfer time for enzymes can
only be reduced by applying mechanical energy that induces fl ow within
the intra-yarn pores, consequently resulting in a smaller stagnant core and
more convective transfer. The way to achieve this is by squeezing the
fabric to force water to flow through the intra-yarn capillaries. This can be

achieved when the textile is running over rollers or by passing between
squeezing rollers. The mechanical energy delivered by these systems and
their effect on the mass transfer inside the textile is unknown. To enable
the squeezing action in textile treatment systems to be measured we have
developed a model that relates the performance of wet textile equipment
to a squeezing factor α.

© Woodhead Publishing Limited, 2010