Page 124 - Aerodynamics for Engineering Students

Potential flow 107

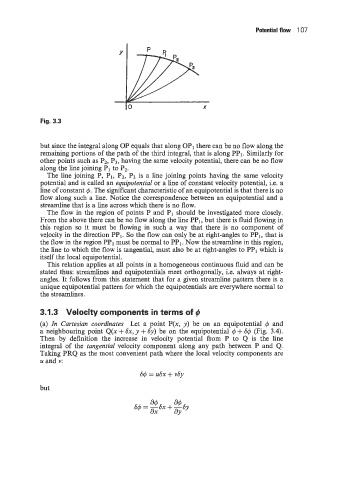
Fig. 3.3

but since the integral along OP equals that along OP1 there can be no flow along the
remaining portions of the path of the third integral, that is along PPI. Similarly for
other points such as P2, P3, having the same velocity potential, there can be no flow
along the line joining PI to Pz.
The line joining P, PI, P2, P3 is a line joining points having the same velocity
potential and is called an equipotential or a line of constant velocity potential, i.e. a
line of constant 4. The significant characteristic of an equipotential is that there is no
flow along such a line. Notice the correspondence between an equipotential and a
streamline that is a line across which there is no flow.
The flow in the region of points P and PI should be investigated more closely.
From the above there can be no flow along the line PPI, but there is fluid flowing in
this region so it must be flowing in such a way that there is no component of
velocity in the direction PPI. So the flow can only be at right-angles to PPI, that is
the flow in the region PPI must be normal to PPI. Now the streamline in this region,
the line to which the flow is tangential, must also be at right-angles to PPI which is
itself the local equipotential.
This relation applies at all points in a homogeneous continuous fluid and can be
stated thus: streamlines and equipotentials meet orthogonally, i.e. always at right-
angles. It follows from this statement that for a given streamline pattern there is a
unique equipotential pattern for which the equipotentials are everywhere normal to
the streamlines.

3.1.3 Velocity components in terms of @
(a) In Cartesian coordinates Let a point P(x, y) be on an equipotential 4 and
a neighbouring point Q(x + 6x, y + Sy) be on the equipotential 4 + 64 (Fig. 3.4).
Then by definition the increase in velocity potential from P to Q is the line
integral of the tangential velocity component along any path between P and Q.
Taking PRQ as the most convenient path where the local velocity components are
u and v:
64 = usx + vsy

but
a4 *
64 = -sx + -6y
ax ay