Page 284 - Aerodynamics for Engineering Students

Finite wing theory 267

The total lift acting on a slender delta wing is assumed to be the sum of the vortex
and potential flow lifts. Thus
CL = Kpsinacosa, + Kvsin'acosa (5.80)

w- vortex lift
where Kp and KV are coefficients which are given approximately by 2n tan A and
1.95 respectively, or alternatively can be determined from experimental data. The
potential-flow term dominates at small angles of incidence and the vortex lift at
higher incidence. The mechanism for generating the vortex lift is probably nonlinear
to a significant extent, so there is really no theoretical justification for simply sum-
ming the two effects. Nevertheless, Eqn (5.80) fits the experimental data reasonably
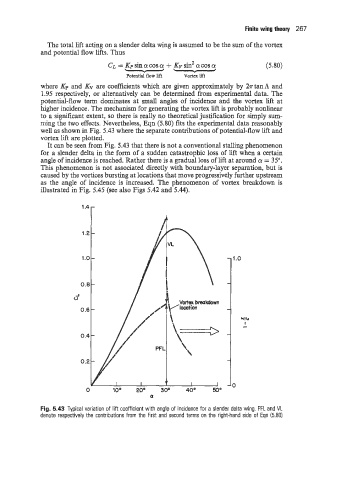
well as shown in Fig. 5.43 where the separate contributions of potential-flow lift and
vortex lift are plotted.
It can be seen from Fig. 5.43 that there is not a conventional stalling phenomenon
for a slender delta in the form of a sudden catastrophic loss of lift when a certain
angle of incidence is reached. Rather there is a gradual loss of lift at around a = 35".
This phenomenon is not associated directly with boundary-layer separation, but is
caused by the vortices bursting at locations that move progressively further upstream
as the angle of incidence is increased. The phenomenon of vortex breakdown is
illustrated in Fig. 5.45 (see also Figs 5.42 and 5.44).

1

1.0

Vortex breakdown
/location
i. *IC,
\- c
I

1

- 0
' 40' 50'
a
Fig. 5.43 Typical variation of lift coefficient with angle of incidence for a slender delta wing. PFL and VL
denote respectively the contributions from the first and second terms on the right-hand side of Eqn (5.80)