Page 58 - Aircraft Stuctures for Engineering Student

2.6 Bending of an end-loaded cantilever 43
--.--r-- ------
-?.- -vI-nr.---- -
-E”i&3acements
Having found the components of stress, Eqs (1.47) (for the case of plane stress) are
used to determine the components of strain. The displacements follow from Eqs
(1.27) and (1.28). The integration of Eqs (1.27) yields solutions of the form
u 1 + u - by (2.10)
E,X
v = ~~y + c + bx (2.11)
in which a, b and c are constants representing movement of the body as a whole or
rigid body displacements. Of these a and c represent pure translatory motions of
the body while b is a small angular rotation of the body in the xy plane. If we
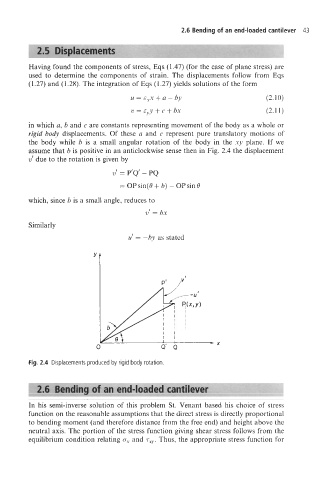
assume that b is positive in an anticlockwise sense then in Fig. 2.4 the displacement
v’ due to the rotation is given by

V‘ = P’Q’ - PQ
= OP sin(8 + b) - OP sin 8
which, since b is a small angle, reduces to

V’ = hx
Similarly
u’ = -by as stated

P‘ /” I

0

Fig. 2.4 Displacements produced by rigid body rotation.

In his semi-inverse solution of this problem St. Venant based his choice of stress
function on the reasonable assumptions that the direct stress is directly proportional
to bending moment (and therefore distance from the free end) and height above the
neutral axis. The portion of the stress function giving shear stress follows from the
equilibrium condition relating a, and T,~. Thus, the appropriate stress function for