Page 594 - Aircraft Stuctures for Engineering Student

13.4 Introduction to 'flutter' 575

section torsional divergence speed, any torsional oscillation produced, say, by a gust
will decay. Also, from Eq. (13.67), it would appear that a vertical oscillation could be
maintained by the incidence term Loo. However, rotational oscillations, as we have
seen from Eq. (13.68), decay so that the lift force L,a is a decaying force and
cannot maintain any vertical oscillation.
In practice it is not always possible to prevent flutter by eliminating coupling terms.
However, increasing structural stiffness, although carrying the penalty of increased
weight, can raise the value of V, above the operating speed range. Further, arranging
for the centre of gravity of the wing section to be as close as possible to and forward of
the flexural axis is beneficial. Thus, wing mounted jet engines are housed in pods well
ahead of the flexural axis of the wing.

The previous analysis has been concerned with the flutter of a simple two degrees of
freedom model. In practice the structure of an aircraft can oscillate in many different
ways. For example, a wing has fundamental bending and torsional modes of
oscillation on which secondary or overtone modes of oscillation are superimposed.
Also it is possible for fuselage bending oscillations to produce changes in wing
camber thereby affecting wing lift and for control surfaces oscillating about their
hinges to produce aerodynamic forces on the main surfaces.
The equations of motion for an actual aircraft are therefore complex with a number
N, say, of different motions being represented (N can be as high as 12). There are,
therefore, N equations of motion which are aerodynamically coupled. At a given
speed, solution of these N equations yields N different values of S + iw corresponding
to the N modes of oscillation. Again, as in the simple two degrees of freedom case, the
critical flutter speed for each mode may be found by calculating S for a range of speeds
and determining the value of speed at which S = 0.
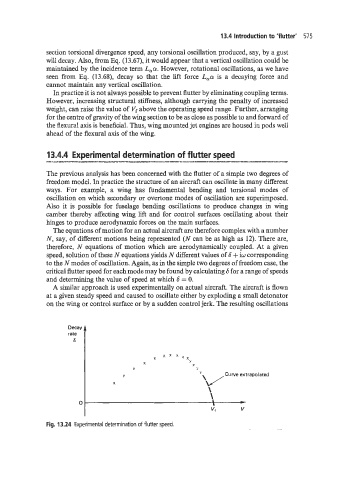
A similar approach is used experimentally on actual aircraft. The aircraft is flown
at a given steady speed and caused to oscillate either by exploding a small detonator
on the wing or control surface or by a sudden control jerk. The resulting oscillations

ra: I
Decay

Fig. 13.24 Experimental determination of flutter speed.