Page 68 -

42 Chapter 2 ■ Edge-Detection Techniques

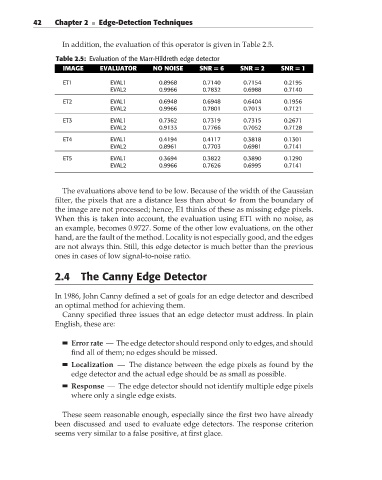
In addition, the evaluation of this operator is given in Table 2.5.
Table 2.5: Evaluation of the Marr-Hildreth edge detector
IMAGE EVALUATOR NO NOISE SNR = 6 SNR = 2 SNR = 1
ET1 EVAL1 0.8968 0.7140 0.7154 0.2195
EVAL2 0.9966 0.7832 0.6988 0.7140
ET2 EVAL1 0.6948 0.6948 0.6404 0.1956
EVAL2 0.9966 0.7801 0.7013 0.7121
ET3 EVAL1 0.7362 0.7319 0.7315 0.2671
EVAL2 0.9133 0.7766 0.7052 0.7128
ET4 EVAL1 0.4194 0.4117 0.3818 0.1301
EVAL2 0.8961 0.7703 0.6981 0.7141
ET5 EVAL1 0.3694 0.3822 0.3890 0.1290
EVAL2 0.9966 0.7626 0.6995 0.7141

Theevaluations abovetendtobelow. Because of thewidth of theGaussian
filter, the pixels that are a distance less than about 4σ from the boundary of
the image are not processed; hence, E1 thinks of these as missing edge pixels.
When this is taken into account, the evaluation using ET1 with no noise, as
an example, becomes 0.9727. Some of the other low evaluations, on the other
hand, are the fault of the method. Locality is not especially good, and the edges
are not always thin. Still, this edge detector is much better than the previous
ones in cases of low signal-to-noise ratio.

2.4 The Canny Edge Detector

In 1986, John Canny defined a set of goals for an edge detector and described
an optimal method for achieving them.
Canny specified three issues that an edge detector must address. In plain
English, these are:

Error rate — The edge detector should respond only to edges, and should
find all of them; no edges should be missed.
Localization — The distance between the edge pixels as found by the
edge detector and the actual edge should be as small as possible.
Response — The edge detector should not identify multiple edge pixels
where only a single edge exists.

These seem reasonable enough, especially since the first two have already
been discussed and used to evaluate edge detectors. The response criterion
seems very similar to a false positive, at first glace.