Page 114 -

94 CHAPTER 3 LINEAR PROGRAMMING: SENSITIVITY ANALYSIS AND INTERPRETATION OF SOLUTION

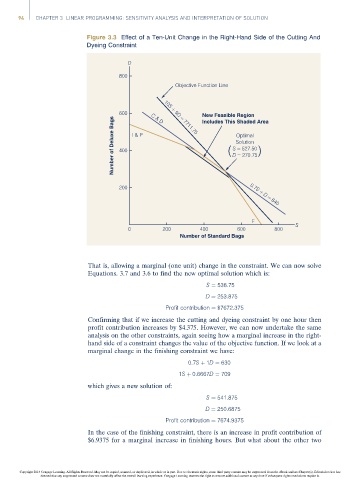
Figure 3.3 Effect of a Ten-Unit Change in the Right-Hand Side of the Cutting And
Dyeing Constraint

D
800
Objective Function Line

600 C & D 10S + 9D = 7711.75 New Feasible Region
Number of Deluxe Bags 400 I & P ( S = 527.50 )
Includes This Shaded Area
Optimal
Solution
D = 270.75

200 0.7S + D = 640

F
0 200 400 600 800 S
Number of Standard Bags

That is, allowing a marginal (one unit) change in the constraint. We can now solve
Equations. 3.7 and 3.6 to find the new optimal solution which is:

S ¼ 538:75
D ¼ 253:875
Profit contribution ¼ $7672:375
Confirming that if we increase the cutting and dyeing constraint by one hour then
profit contribution increases by $4.375. However, we can now undertake the same
analysis on the other constraints, again seeing how a marginal increase in the right-
hand side of a constraint changes the value of the objective function. If we look at a
marginal change in the finishing constraint we have:
0:7S þ 1D ¼ 630

1S þ 0:6667D ¼ 709
which gives a new solution of:
S ¼ 541:875
D ¼ 250:6875

Profit contribution ¼ 7674:9375
In the case of the finishing constraint, there is an increase in profit contribution of
$6.9375 for a marginal increase in finishing hours. But what about the other two

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.