Page 290 -

270 CHAPTER 6 SIMPLEX-BASED SENSITIVITY ANALYSIS AND DUALITY

Dual Problem Given the availability of each resource, determine the per-unit value
such that the total value of the resources used is minimized. Constraints require the
resource value per unit to be greater than or equal to the value of each unit of
output.

Using the Dual to Identify the Primal Solution

At the beginning of this section, we mentioned that an important feature of the
primal–dual relationship is that when an optimal solution is reached, the value of the
optimal solution for the primal problem is the same as the value of the optimal
solution for the dual problem; see property 1. However, the question remains: if we
solve only the dual problem, can we identify the optimal values for the primal
variables?
Recall that in Section 6.1 we showed that when a primal problem is solved by the
Simplex method, the optimal values of the primal variables appear in the right-most
column of the final tableau, and the dual prices (values of the dual variables) are
found in the z j row. The final tableau of the dual problem provides the optimal
values of the dual variables, and therefore the values of the primal variables should
be found in the z j row of the optimal dual tableau. This result is, in fact, the case and
is formally stated as property 2.
Property 2
Given the simplex tableau corresponding to the optimal dual solution, the
optimal values of the primal decision variables are given by the z j entries for
the surplus variables; furthermore, the optimal values of the primal slack
variables are given by the negative of the c j – z j entries for the u j variables.
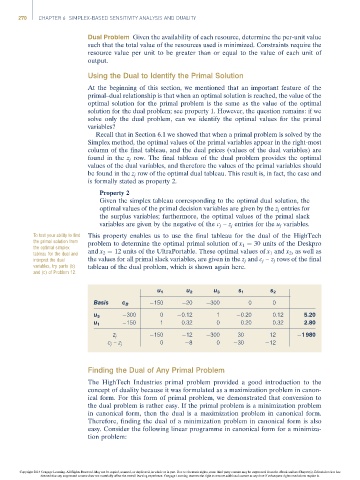
To test your ability to find This property enables us to use the final tableau for the dual of the HighTech
the primal solution from problem to determine the optimal primal solution of x 1 ¼ 30 units of the Deskpro
the optimal simplex
tableau for the dual and and x 2 ¼ 12 units of the UltraPortable. These optimal values of x 1 and x 2 , as well as
interpret the dual the values for all primal slack variables, are given in the z j and c j – z j rows of the final
variables, try parts (b) tableau of the dual problem, which is shown again here.
and (c) of Problem 12.

u 1 u 2 u 3 s 1 s 2
Basis c B 150 20 300 0 0
300 0 0.12 1 0.20 0.12 5.20
u 3
150 1 0.32 0 0.20 0.32 2.80
u 1
150 12 300 30 12 1 980
z j
0 8 0 30 12
c j – z j

Finding the Dual of Any Primal Problem
The HighTech Industries primal problem provided a good introduction to the
concept of duality because it was formulated as a maximization problem in canon-
ical form. For this form of primal problem, we demonstrated that conversion to
the dual problem is rather easy. If the primal problem is a minimization problem
in canonical form, then the dual is a maximization problem in canonical form.
Therefore, finding the dual of a minimization problem in canonical form is also
easy. Consider the following linear programme in canonical form for a minimiza-
tion problem:

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.