Page 329 -

ASSIGNMENT PROBLEM: A SPECIAL-PURPOSE SOLUTION PROCEDURE 309

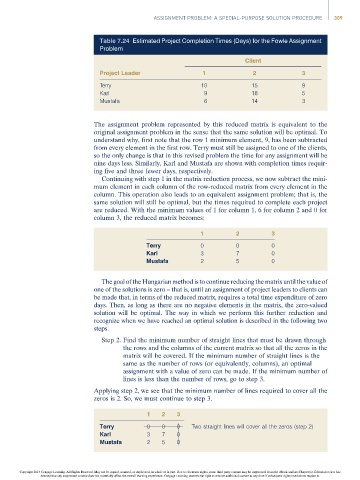
Table 7.24 Estimated Project Completion Times (Days) for the Fowle Assignment
Problem
Client

Project Leader 1 2 3
Terry 10 15 9
Karl 9 18 5
Mustafa 6 14 3

The assignment problem represented by this reduced matrix is equivalent to the
original assignment problem in the sense that the same solution will be optimal. To
understand why, first note that the row 1 minimum element, 9, has been subtracted
from every element in the first row. Terry must still be assigned to one of the clients,
so the only change is that in this revised problem the time for any assignment will be
nine days less. Similarly, Karl and Mustafa are shown with completion times requir-
ing five and three fewer days, respectively.
Continuing with step 1 in the matrix reduction process, we now subtract the mini-
mum element in each column of the row-reduced matrix from every element in the
column. This operation also leads to an equivalent assignment problem; that is, the
same solution will still be optimal, but the times required to complete each project
are reduced. With the minimum values of 1 for column 1, 6 for column 2 and 0 for
column 3, the reduced matrix becomes:

1 2 3
Terry 0 0 0
Karl 3 7 0
Mustafa 2 5 0

The goal of the Hungarian method is to continue reducing the matrix until the value of
one of the solutions is zero – that is, until an assignment of project leaders to clients can
be made that, in terms of the reduced matrix, requires a total time expenditure of zero
days. Then, as long as there are no negative elements in the matrix, the zero-valued
solution will be optimal. The way in which we perform this further reduction and
recognize when we have reached an optimal solution is described in the following two
steps.
Step 2. Find the minimum number of straight lines that must be drawn through
the rows and the columns of the current matrix so that all the zeros in the
matrix will be covered. If the minimum number of straight lines is the
same as the number of rows (or equivalently, columns), an optimal
assignment with a value of zero can be made. If the minimum number of
lines is less than the number of rows, go to step 3.
Applying step 2, we see that the minimum number of lines required to cover all the
zeros is 2. So, we must continue to step 3.

1 2 3

Terry 0 0 0 Two straight lines will cover all the zeros (step 2)
Karl 3 7 0
Mustafa 2 5 0

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.