Page 334 -

314 CHAPTER 7 TRANSPORTATION, ASSIGNMENT AND TRANSSHIPMENT PROBLEMS

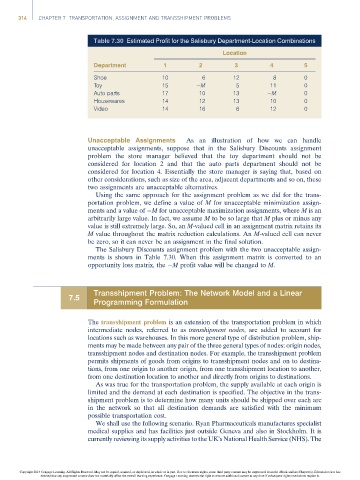
Table 7.30 Estimated Profit for the Salisbury Department-Location Combinations
Location
Department 1 2 3 4 5

Shoe 10 6 12 8 0
Toy 15 M 5 11 0
Auto parts 17 10 13 M 0
Housewares 14 12 13 10 0
Video 14 16 6 12 0

Unacceptable Assignments As an illustration of how we can handle
unacceptable assignments, suppose that in the Salisbury Discounts assignment
problem the store manager believed that the toy department should not be
considered for location 2 and that the auto parts department should not be
considered for location 4. Essentially the store manager is saying that, based on
other considerations, such as size of the area, adjacent departments and so on, these
two assignments are unacceptable alternatives.
Using the same approach for the assignment problem as we did for the trans-
portation problem, we define a value of M for unacceptable minimization assign-
ments and a value of M for unacceptable maximization assignments, where M is an
arbitrarily large value. In fact, we assume M to be so large that M plus or minus any
value is still extremely large. So, an M-valued cell in an assignment matrix retains its
M value throughout the matrix reduction calculations. An M-valued cell can never
be zero, so it can never be an assignment in the final solution.
The Salisbury Discounts assignment problem with the two unacceptable assign-
ments is shown in Table 7.30. When this assignment matrix is converted to an
opportunity loss matrix, the M profit value will be changed to M.

Transshipment Problem: The Network Model and a Linear
7.5
Programming Formulation

The transshipment problem is an extension of the transportation problem in which
intermediate nodes, referred to as transshipment nodes, are added to account for
locations such as warehouses. In this more general type of distribution problem, ship-
ments may be made between any pair of the three general types of nodes: origin nodes,
transshipment nodes and destination nodes. For example, the transshipment problem
permits shipments of goods from origins to transshipment nodes and on to destina-
tions, from one origin to another origin, from one transshipment location to another,
from one destination location to another and directly from origins to destinations.
As was true for the transportation problem, the supply available at each origin is
limited and the demand at each destination is specified. The objective in the trans-
shipment problem is to determine how many units should be shipped over each arc
in the network so that all destination demands are satisfied with the minimum
possible transportation cost.
We shall use the following scenario. Ryan Pharmaceuticals manufactures specialist
medical supplies and has facilities just outside Geneva and also in Stockholm. It is
currently reviewing its supply activities to the UK’s National Health Service (NHS). The

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.