Page 337 -

TRANSSHIPMENT PROBLEM: THE NETWORK MODEL AND A LINEAR PROGRAMMING FORMULATION 317

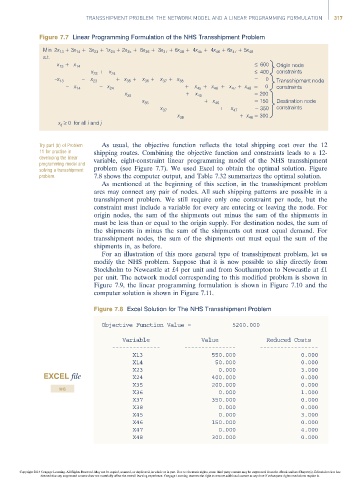
Figure 7.7 Linear Programming Formulation of the NHS Transshipment Problem

Min 2x 13 + 3x 14 + 3x 23 + 1x 24 + 2x 35 + 6x 36 + 3x 37 + 6x 38 + 4x 45 + 4x 46 + 6x 47 + 5x 48
s.t.
600
x 13 + x 14 Origin node
x 23 + x 24 400 constraints
–x 13 – x 23 + x 35 + x 36 + x 37 + x 38 = 0 Transshipment node
– x 14 – x 24 + x 45 + x 46 + x 47 + x 48 = 0 constraints
x 35 + x 45 = 200
x 36 + x 46 = 150 Destination node
x 37 + x 47 = 350 constraints
x 38 + x 48 = 300
x ij 0 for all i and j

Try part (b) of Problem As usual, the objective function reflects the total shipping cost over the 12
11 for practise in shipping routes. Combining the objective function and constraints leads to a 12-
developing the linear variable, eight-constraint linear programming model of the NHS transshipment
programming model and
solving a transshipment problem (see Figure 7.7). We used Excel to obtain the optimal solution. Figure
problem. 7.8 shows the computer output, and Table 7.32 summarizes the optimal solution.
As mentioned at the beginning of this section, in the transshipment problem
arcs may connect any pair of nodes. All such shipping patterns are possible in a
transshipment problem. We still require only one constraint per node, but the
constraint must include a variable for every arc entering or leaving the node. For
origin nodes, the sum of the shipments out minus the sum of the shipments in
must be less than or equal to the origin supply. For destination nodes, the sum of
the shipments in minus the sum of the shipments out must equal demand. For
transshipment nodes, the sum of the shipments out must equal the sum of the
shipments in, as before.
For an illustration of this more general type of transshipment problem, let us
modify the NHS problem. Suppose that it is now possible to ship directly from
Stockholm to Newcastle at £4 per unit and from Southampton to Newcastle at £1
per unit. The network model corresponding to this modified problem is shown in
Figure 7.9, the linear programming formulation is shown in Figure 7.10 and the
computer solution is shown in Figure 7.11.

Figure 7.8 Excel Solution for The NHS Transshipment Problem

Objective Function Value = 5200.000

Variable Value Reduced Costs
-------------- --------------- -----------------
X13 550.000 0.000
X14 50.000 0.000
X23 0.000 3.000
EXCEL file X24 400.000 0.000
X35 200.000 0.000
NHS
X36 0.000 1.000
X37 350.000 0.000
X38 0.000 0.000
X45 0.000 3.000
X46 150.000 0.000
X47 0.000 4.000
X48 300.000 0.000

Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.