Page 360 -
P. 360
340 CHAPTER 7 TRANSPORTATION, ASSIGNMENT AND TRANSSHIPMENT PROBLEMS
The linear programming model is developed in the bottom portion of the
worksheet. As with all linear programmes the model has four key elements:
the decision variables, the objective function, the constraint left-hand sides and
the constraint right-hand sides. For an assignment problem the decision variables
indicate whetherapersonisassignedtoatask (witha1for yesor0 forno);the
objective function is the total cost of all assignments; the constraint left-
hand sides are the number of tasks that are assigned to each person and the
number of people that are assigned to each task; and the right-hand sides are
the number of tasks each person can handle (1) and the number of people each
task requires (1).
The worksheet formulation and solution for the Fowle Marketing Research
Problem (see Section 7.3) are shown in Figure 7.16.
Formulation
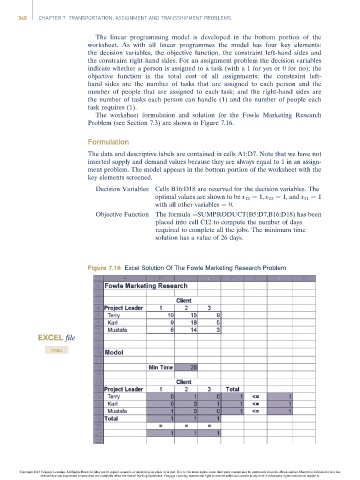
The data and descriptive labels are contained in cells A1:D7. Note that we have not
inserted supply and demand values because they are always equal to 1 in an assign-
ment problem. The model appears in the bottom portion of the worksheet with the
key elements screened.
Decision Variables Cells B16:D18 are reserved for the decision variables. The
optimal values are shown to be x 12 ¼ 1, x 23 ¼ 1, and x 31 ¼ 1
with all other variables ¼ 0.
Objective Function The formula ¼SUMPRODUCT(B5:D7,B16:D18) has been
placed into cell C12 to compute the number of days
required to complete all the jobs. The minimum time
solution has a value of 26 days.
Figure 7.16 Excel Solution Of The Fowle Marketing Research Problem
EXCEL file
FOWLE
Copyright 2014 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has
deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it.