Page 269 - An Introduction to Microelectromechanical Systems Engineering

248 Packaging and Reliability Considerations for MEMS

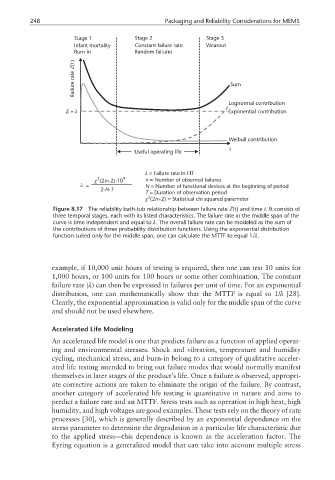
Stage 1 Stage 2 Stage 3
Infant mortality Constant failure rate Wearout
Burn in Random failures
)
Zt (
rate
Failure Sum

Lognormal contribution
Z= λ Exponential contribution

Weibull contribution
t
Useful operating life

λ = Failure rate in FIT
2 9
χ (2 +2)·10n n = Number of observed failures
λ = N = Number of functional devices at the beginning of period
2· ·NT
T = Duration of observation period
2
n
χ (2 +2) = Statistical chi squared parameter
Figure 8.17 The reliability bath-tub relationship between failure rate Z(t) and time t. It consists of
three temporal stages, each with its listed characteristics. The failure rate in the middle span of the
curve is time independent and equal to λ. The overall failure rate can be modeled as the sum of
the contributions of three probability distribution functions. Using the exponential distribution
function suited only for the middle span, one can calculate the MTTF to equal 1/λ.

example, if 10,000 unit hours of testing is required, then one can test 10 units for
1,000 hours, or 100 units for 100 hours or some other combination. The constant
failure rate (λ) can then be expressed in failures per unit of time. For an exponential
distribution, one can mathematically show that the MTTF is equal to 1/λ [28].
Clearly, the exponential approximation is valid only for the middle span of the curve
and should not be used elsewhere.

Accelerated Life Modeling
An accelerated life model is one that predicts failure as a function of applied operat-
ing and environmental stresses. Shock and vibration, temperature and humidity
cycling, mechanical stress, and burn-in belong to a category of qualitative acceler-
ated life testing intended to bring out failure modes that would normally manifest
themselves in later stages of the product’s life. Once a failure is observed, appropri-
ate corrective actions are taken to eliminate the origin of the failure. By contrast,
another category of accelerated life testing is quantitative in nature and aims to
predict a failure rate and an MTTF. Stress tests such as operation in high heat, high
humidity, and high voltages are good examples. These tests rely on the theory of rate
processes [30], which is generally described by an exponential dependence on the
stress parameter to determine the degradation in a particular life characteristic due
to the applied stress—this dependence is known as the acceleration factor. The
Eyring equation is a generalized model that can take into account multiple stress