Page 139 - Analysis and Design of Energy Geostructures

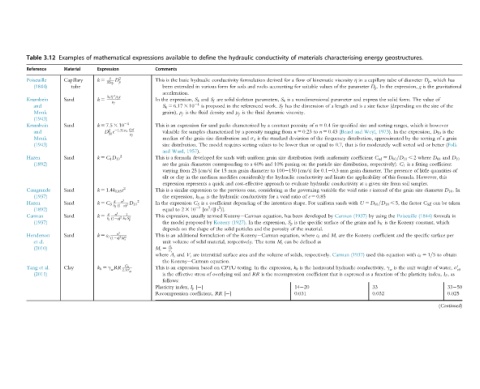
has gravitational the the grain (Folk D 10 and of D 10 .In taken in per obtain σ 0 v0 water, I P ,as 33 50 0.025 (Continued)
which of of size however is D 50 a of better D 60 coefficient quantities this diameter be can formula which surface to of index,
D p , the is g value The the on is which expression, sorting or soil where fitting little of However, samples. size C S g (1844) constant, specific c 0 5 1=5 weight plasticity
geostructures. diameter of tube expression, the form. solid (depending ranges, the In the by approximated sorted well C ud 5 D 60 =D 10 , 2 a is C 1 presence formula. this soil from grain the of factor the Poiseuille the Kozeny the the and with equation unit the is γ w the of

energy capillary a in In D p . parameter the express factor size a is sorting and size 1973). Weyl, distribution, moderately for coefficient respectively). The diameter. of applicability site given a at instead e ratio U 5 D 60 =D 10 , 5, using by (1937) is h K and grains coefficient Kozeny this used conductivity, function a as 33 0.032

characterising η viscosity the of and parameter and length a of specified for and (Beard n 5 0.43 frequency is that 0.7, to uniformity distribution, size grain 0.1 0.3 mm the limits and conductivity void the variable with sands Carman by the of surface the are M s (1937) Carman hydraulic expressed is that

materials kinematic of values suitable nondimensional dimension n 5 0:4 of to n 5 0.23 the of equal or than (with particle the on for [cm/s] conductivity hydraulic governing e 5 0:85 of uniform For developed specific the material. and c 0 where as defined respectively. horizontal the is coefficient 14 20

of flow a for for a is S k the has viscosity. porosity from deviation lower distribution passing 100 150 hydraulic evaluate to the as ratio void shape. been has is S p the of equation, be can solids, of k h recompression 0.031
conductivity derived accounting rocks parameters, S f work. dynamic fluid constant a by ranging standard the is be to values size grain 10% and 60% to diameter the approach considering a for interstices the of equation, expression, the porosity the and Kozeny Carman M s term The volume the expression, the the is

hydraulic formulation and soils for skeleton referenced the the is μ f characterised porosity a by σ d and sorting requires uniform with a to grain considerably cost-effective one, previous conductivity depending Kozeny Carman In (1927). particles the respectively. and area In testing. RR and soil

the conductivity form solid are in proposed and density packs characterised distribution model sands for corresponding 15 mm for modifies and quick the to hydraulic the coefficient termed Kozeny solid the of material, surface equation. CPTU on overlying [ ] RR
define various S f and is fluid sand for size The developed diameters [cm/s] medium a expression is k 0:85 a is [m 5 /(J s 2 )]. by of shape formulation solid interstitial based of coefficient,

to hydraulic in S k the is expression samples grain the 1957). 25 the in represents C S 2 3 10 27 usually proposed the additional of are V s Kozeny Carman expression stress [ ] I p
available Comments basic the is extended been acceleration. expression, the S k 5 6:17 3 10 24 ρ f grains), an is for valuable of median distribution. size Ward, and formula a is grain the are from varying clay or silt expression similar a is expression, the expression the to equal expression, model the on depends an is volume unit A s V s and A s the an

expressions This In This ρ f g μ f This This In This This M s 5 where This

mathematical Expression g D 2 k 5 p 32η f S k S f 2 ρ f g k 5 μ f k 5 7:5 3 10 24 D 2 50 e 21:31σ d k 5 C 1 D 10 2 k 5 1:4k 0:85 e 2 g n 3 k 5 C S η f 12nÞ 2 D 10 2 ð g 1 n 3 k 5 12nÞ 2 h K S 2 p ð η f n 3 k 5 c 0 ð12nÞ 2 M 2 s C h k h 5 γ w RR 2:3σ 0 v0

of
Examples Material Capillary tube Sand Sand Sand Sand Sand Sand Sand Clay

3.12 al.
Table Reference Poiseuille (1844) Krumbein and Monk (1943) Krumbein and Monk (1943) Hazen (1892) Casagrande (1937) Hazen (1892) Carman (1937) Henderson al. et (2010) et Tang (2011)