Page 186 - Analysis and Design of Energy Geostructures

Deformation in the context of energy geostructures 159

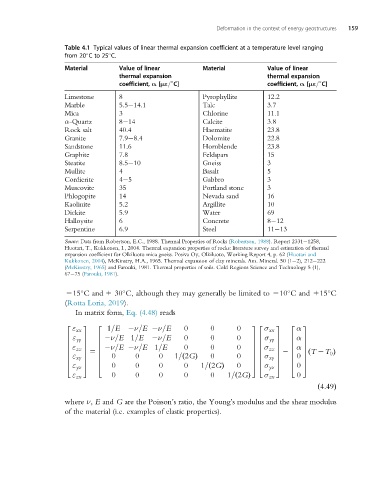
Table 4.1 Typical values of linear thermal expansion coefficient at a temperature level ranging
from 20 Cto25 C.

Material Value of linear Material Value of linear
thermal expansion thermal expansion
coefficient, α [με= C] coefficient, α [με= C]

Limestone 8 Pyrophyllite 12.2
Marble 5.5 14.1 Talc 3.7
Mica 3 Chlorine 11.1
α-Quartz 8 14 Calcite 3.8
Rock salt 40.4 Haematite 23.8
Granite 7.9 8.4 Dolomite 22.8
Sandstone 11.6 Hornblende 23.8
Graphite 7.8 Feldspars 15
Steatite 8.5 10 Gneiss 3
Mullite 4 Basalt 5
Cordierite 4 5 Gabbro 3
Muscovite 35 Portland stone 3
Phlogopite 14 Nevada sand 16
Kaolinite 5.2 Argillite 10
Dickite 5.9 Water 69
Halloysite 6 Concrete 8 12
Serpentine 6.9 Steel 11 13
Source: Data from Robertson, E.C., 1988. Thermal Properties of Rocks (Robertson, 1988). Report 2331 1258,
Huotari, T., Kukkonen, I., 2004. Thermal expansion properties of rocks: literature survey and estimation of thermal
expansion coefficient for Olkiluoto mica gneiss. Posiva Oy, Olkiluoto, Working Report 4, p. 62 (Huotari and
Kukkonen, 2004), McKinstry, H.A., 1965. Thermal expansion of clay minerals. Am. Mineral. 50 (1 2), 212 222
(McKinstry, 1965) and Farouki, 1981. Thermal properties of soils. Cold Regions Science and Technology 5 (1),
67 75 (Farouki, 1981).

215 Cand 1 30 C, although they may generally be limited to 210 Cand 115 C

(Rotta Loria, 2019).
In matrix form, Eq. (4.48) reads
0 0 0
2 3 2 32 3 2 α 3
1=E 2ν=E 2ν=E σ xx
ε xx
0 0 0
2ν=E 1=E 2ν=E
6
6 ε yy 7 6 7 σ yy 7 6 α 7
0 0 0
6 7 6 76 7 6 7
6
6 ε zz 7 6 2ν=E 2ν=E 1=E 7 σ zz 7 6 α 7
7 T 2T 0 Þ
ð
0 0 0 1=ð2GÞ 0 0
6 756 76 726
6
6 ε xy 7 6 7 σ xy 7 6 0 7
0 0 0 0 1=ð2GÞ 0 σ yz 0
4 5 4 54 5 4 5
ε yz
0 0 0 0 0 1=ð2GÞ σ zx 0
ε zx
ð4:49Þ
where ν, E and G are the Poisson’s ratio, the Young’s modulus and the shear modulus
of the material (i.e. examples of elastic properties).