Page 200 - Analysis and Design of Energy Geostructures

Deformation in the context of energy geostructures 173

potential function. According to Yu (2006), if the unit normal to the plastic potential
approaches a finite number of linearly independent limiting values as the stress point
approaches the singular point in question, the following generalised flow rule initially
proposed by Koiter (1953) can be considered

N
X
dε 5 dλ p @g k ð4:87Þ
p
ij k
k51 @σ ij
where dλ are nonnegative and @g k =@σ ij are the linearly independent gradients.
p
k
In general, the plastic potential function may or may not be the same as the yield
function. If the plastic potential is assumed to be the same as the yield function (i.e.
f 5 g), the plastic flow rule is called associated (or normality) flow rule. In contrast, if the
potential is assumed to differ compared to the yield function (i.e. f 6¼ g), the plastic
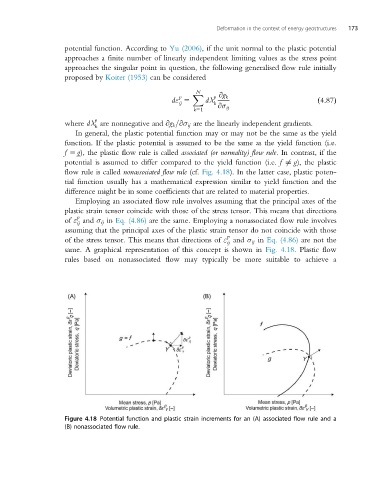
flow rule is called nonassociated flow rule (cf. Fig. 4.18). In the latter case, plastic poten-
tial function usually has a mathematical expression similar to yield function and the
difference might be in some coefficients that are related to material properties.
Employing an associated flow rule involves assuming that the principal axes of the
plastic strain tensor coincide with those of the stress tensor. This means that directions
of ε and σ ij in Eq. (4.86) are the same. Employing a nonassociated flow rule involves
p
ij
assuming that the principal axes of the plastic strain tensor do not coincide with those
of the stress tensor. This means that directions of ε and σ ij in Eq. (4.86) are not the
p
ij
same. A graphical representation of this concept is shown in Fig. 4.18. Plastic flow
rules based on nonassociated flow may typically be more suitable to achieve a

Figure 4.18 Potential function and plastic strain increments for an (A) associated flow rule and a
(B) nonassociated flow rule.