Page 204 - Analysis and Design of Energy Geostructures

Deformation in the context of energy geostructures 177

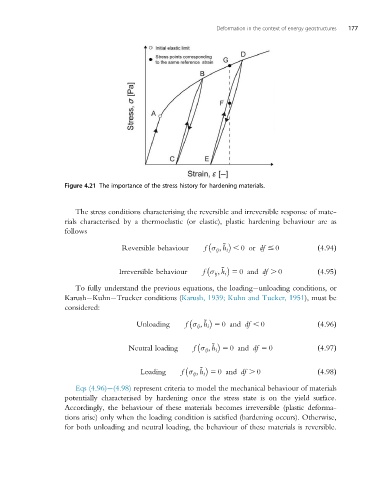
Figure 4.21 The importance of the stress history for hardening materials.

The stress conditions characterising the reversible and irreversible response of mate-
rials characterised by a thermoelastic (or elastic), plastic hardening behaviour are as
follows
~
Reversible behaviour f σ ij ; h i , 0or df # 0 ð4:94Þ

~
Irreversible behaviour f σ ij ; h i 5 0 and df . 0 ð4:95Þ
To fully understand the previous equations, the loading unloading conditions, or
Karush Kuhn Trucker conditions (Karush, 1939; Kuhn and Tucker, 1951), must be
considered:

~
Unloading f σ ij ; h i 5 0 and df , 0 ð4:96Þ

~
Neutral loading f σ ij ; h i 5 0 and df 5 0 ð4:97Þ

~
Loading f σ ij ; h i 5 0 and df . 0 ð4:98Þ
Eqs (4.96) (4.98) represent criteria to model the mechanical behaviour of materials
potentially characterised by hardening once the stress state is on the yield surface.
Accordingly, the behaviour of these materials becomes irreversible (plastic deforma-
tions arise) only when the loading condition is satisfied (hardening occurs). Otherwise,
for both unloading and neutral loading, the behaviour of these materials is reversible.