Page 22 - Analytical Electrochemistry 2d Ed - Jospeh Wang

1-2 FARADAIC PROCESSES 7

of the problem into a domain where a simpler mathematical manipulation is
possible. Details of use of the Laplace transformation are beyond the scope of
this text, and can be found in reference 2. The establishment of proper initial and
boundary conditions (which depend upon the speci®c experiment) is also essential
for this treatment. The current±concentration±time relationships that result from
such treatment will be described below for several relevant experiments.

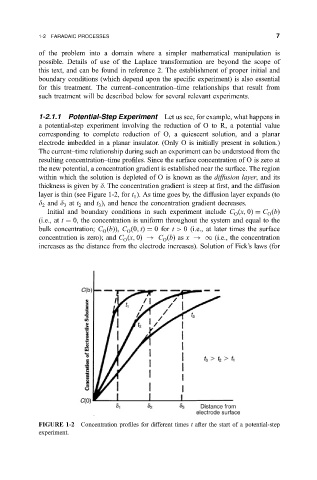
1-2.1.1 Potential-Step Experiment Let us see, for example, what happens in
a potential-step experiment involving the reduction of O to R, a potential value
corresponding to complete reduction of O, a quiescent solution, and a planar
electrode imbedded in a planar insulator. (Only O is initially present in solution.)
The current±time relationship during such an experiment can be understood from the
resulting concentration±time pro®les. Since the surface concentration of O is zero at
the new potential, a concentration gradient is established near the surface. The region
within which the solution is depleted of O is known as the diffusion layer, and its
thickness is given by d. The concentration gradient is steep at ®rst, and the diffusion
layer is thin (see Figure 1-2, for t ). As time goes by, the diffusion layer expands (to
1
d and d at t and t ), and hence the concentration gradient decreases.
3
2
3
2
Initial and boundary conditions in such experiment include C x; 0†ˆ C b†
O
O
(i.e., at t ˆ 0, the concentration is uniform throughout the system and equal to the
bulk concentration; C b†), C 0; t†ˆ 0for t > 0(i.e., at later times the surface
O
O
concentration is zero); and C x; 0†! C b† as x !1 (i.e., the concentration
O
O
increases as the distance from the electrode increases). Solution of Fick's laws (for

FIGURE 1-2 Concentration pro®les for different times t after the start of a potential-step
experiment.