Page 197 - Applied Numerical Methods Using MATLAB

186 NONLINEAR EQUATIONS
6 6

4 4

2 2
x 2 x 3 x 1 x 4 x 3 x 2 x 1
0 0
x 4
−2 −2

−4 −4
1.7 2 2.5 3 1.7 2 2.5 3
(a) Bisection method (b) False position method
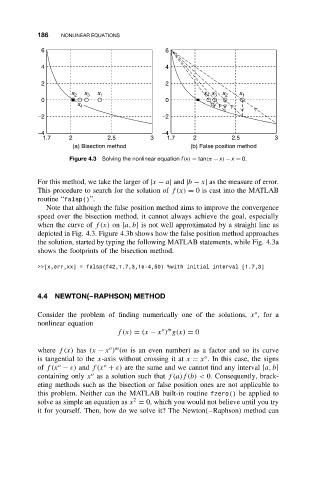
Figure 4.3 Solving the nonlinear equation f(x) = tan(π − x) − x = 0.

For this method, we take the larger of |x − a| and |b − x| as the measure of error.
This procedure to search for the solution of f(x) = 0iscastintothe MATLAB
routine “falsp()”.
Note that although the false position method aims to improve the convergence
speed over the bisection method, it cannot always achieve the goal, especially
when the curve of f(x) on [a, b] is not well approximated by a straight line as
depicted in Fig. 4.3. Figure 4.3b shows how the false position method approaches
the solution, started by typing the following MATLAB statements, while Fig. 4.3a
shows the footprints of the bisection method.

>>[x,err,xx] = falsp(f42,1.7,3,1e-4,50) %with initial interval [1.7,3]

4.4 NEWTON(–RAPHSON) METHOD

o
Consider the problem of finding numerically one of the solutions, x ,for a
nonlinear equation
o m
f(x) = (x − x ) g(x) = 0
o m
where f(x) has (x − x ) (m is an even number) as a factor and so its curve
o
is tangential to the x-axis without crossing it at x = x . In this case, the signs
o
o
of f(x − ε) and f(x + ε) are the same and we cannot find any interval [a, b]
o
containing only x as a solution such that f(a)f (b) < 0. Consequently, brack-
eting methods such as the bisection or false position ones are not applicable to
this problem. Neither can the MATLAB built-in routine fzero() be applied to
2
solve as simple an equation as x = 0, which you would not believe until you try
it for yourself. Then, how do we solve it? The Newton(–Raphson) method can