Page 216 - Applied Numerical Methods Using MATLAB

PROBLEMS 205
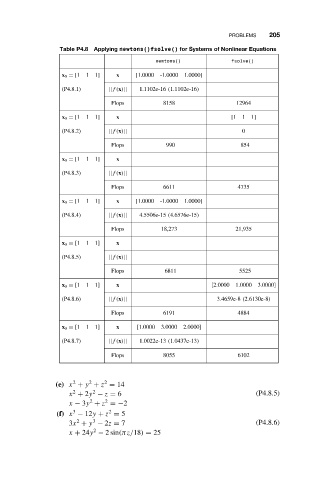
Table P4.8 Applying newtons()fsolve() for Systems of Nonlinear Equations
newtons() fsolve()

x 0 = [1 1 1] x [1.0000 -1.0000 1.0000]
(P4.8.1) ||f(x)|| 1.1102e-16 (1.1102e-16)

Flops 8158 12964
x 0 = [1 1 1] x [111]
(P4.8.2) ||f(x)|| 0

Flops 990 854
x 0 = [1 1 1] x

(P4.8.3) ||f(x)||
Flops 6611 4735
x 0 = [1 1 1] x [1.0000 -1.0000 1.0000]

(P4.8.4) ||f(x)|| 4.5506e-15 (4.6576e-15)
Flops 18,273 21,935

x 0 = [1 1 1] x
(P4.8.5) ||f(x)||

Flops 6811 5525
x 0 = [1 1 1] x [2.0000 1.0000 3.0000]

(P4.8.6) ||f(x)|| 3.4659e-8 (2.6130e-8)
Flops 6191 4884
x 0 = [1 1 1] x [1.0000 3.0000 2.0000]

(P4.8.7) ||f(x)|| 1.0022e-13 (1.0437e-13)
Flops 8055 6102

2
2
2
(e) x + y + z = 14
2
2
x + 2y − z = 6 (P4.8.5)
2
2
x − 3y + z =−2
3
2
(f) x − 12y + z = 5
3
2
3x + y − 2z = 7 (P4.8.6)
2
x + 24y − 2sin(πz/18) = 25