Page 339 - Applied Numerical Methods Using MATLAB

328 OPTIMIZATION
2.5
−6.4(s1) −6.9(s2)
2

1.5

0.0(c) −6.9(e)
1
−5.3(r)
−5.6(e)
0.5
−1.3(s1)
−3.0(a)
0.0(b) −4.5(r)
0
0 0.5 1 1.5 2 2.5 3 3.5
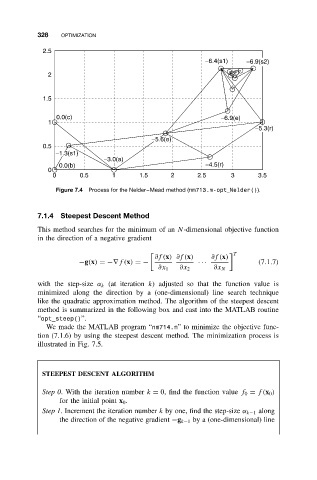
Figure 7.4 Process for the Nelder–Mead method (nm713.m-opt Nelder()).

7.1.4 Steepest Descent Method
This method searches for the minimum of an N-dimensional objective function
in the direction of a negative gradient

∂f (x) ∂f (x) ∂f (x)
T
−g(x) =−∇f(x) =− ·· · (7.1.7)
∂x 1 ∂x 2 ∂x N
with the step-size α k (at iteration k) adjusted so that the function value is
minimized along the direction by a (one-dimensional) line search technique
like the quadratic approximation method. The algorithm of the steepest descent
method is summarized in the following box and cast into the MATLAB routine
“opt_steep()”.
We made the MATLAB program “nm714.m” to minimize the objective func-
tion (7.1.6) by using the steepest descent method. The minimization process is
illustrated in Fig. 7.5.

STEEPEST DESCENT ALGORITHM

Step 0. With the iteration number k = 0, find the function value f 0 = f(x 0 )
for the initial point x 0 .
Step 1. Increment the iteration number k by one, find the step-size α k−1 along
the direction of the negative gradient −g k−1 by a (one-dimensional) line