Page 68 - Applied Numerical Methods Using MATLAB

PROBLEMS 57
(h) Piecewise Polynomial: mkpp()/ppval()
Suppose we have an M × N matrix P, the rows of which denote
M (piecewise) polynomials of degree (N − 1) for different (non-
overlapping) intervals with (M+1) boundary points bb = [b(1)
.. b(M + 1)], where the polynomial coefficients in each row are
supposed to be generated with the interval starting from x = 0. Then
we can use the MATLAB command pp = mkpp(bb,P) to construct a
structure of piecewise polynomials, which can be evaluated by using
ppval(pp).
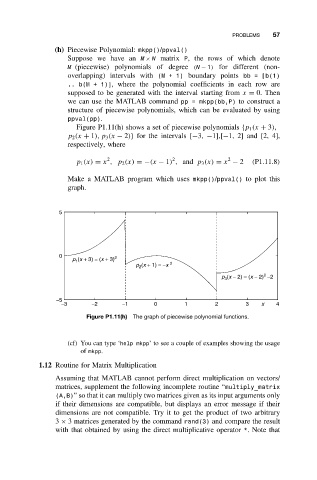
Figure P1.11(h) shows a set of piecewise polynomials {p 1 (x + 3),
p 2 (x + 1), p 3 (x − 2)} for the intervals [−3, −1],[−1, 2] and [2, 4],
respectively, where

2
2
2
p 1 (x) = x ,p 2 (x) =−(x − 1) , and p 3 (x) = x − 2 (P1.11.8)
Make a MATLAB program which uses mkpp()/ppval() to plot this
graph.

5

0
p 1 (x + 3) = (x + 3) 2
p 2 (x + 1) = −x 2
2
p 3 (x − 2) = (x − 2) −2

−5
−3 −2 −1 0 1 2 3 x 4
Figure P1.11(h) The graph of piecewise polynomial functions.

(cf) You can type ‘help mkpp’ to see a couple of examples showing the usage
of mkpp.

1.12 Routine for Matrix Multiplication
Assuming that MATLAB cannot perform direct multiplication on vectors/
matrices, supplement the following incomplete routine “multiply_matrix
(A,B)” so that it can multiply two matrices given as its input arguments only
if their dimensions are compatible, but displays an error message if their
dimensions are not compatible. Try it to get the product of two arbitrary
3 × 3 matrices generated by the command rand(3) and compare the result
with that obtained by using the direct multiplicative operator *. Note that