Page 62 - Applied Probability

30 40 3. Newton’s Method and Scoring 45

Information 20 o o

o
o
o
o
10 o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o o oo oo ooo

0
0.1 0.2 0.3 0.4 0.5
Theta

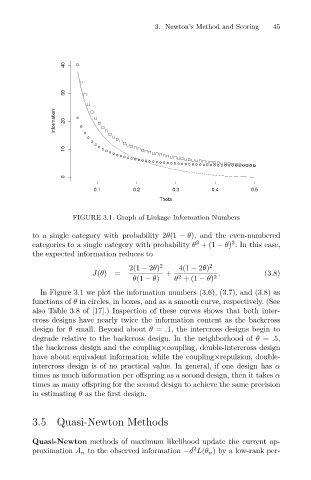
FIGURE 3.1. Graph of Linkage Information Numbers

to a single category with probability 2θ(1 − θ), and the even-numbered
2
2
categories to a single category with probability θ +(1 − θ) . In this case,
the expected information reduces to
2(1 − 2θ) 2 4(1 − 2θ) 2
J(θ) = + . (3.8)
2
θ(1 − θ) θ +(1 − θ) 2
In Figure 3.1 we plot the information numbers (3.6), (3.7), and (3.8) as
functions of θ in circles, in boxes, and as a smooth curve, respectively. (See
also Table 3.8 of [17].) Inspection of these curves shows that both inter-
cross designs have nearly twice the information content as the backcross
design for θ small. Beyond about θ = .1, the intercross designs begin to
degrade relative to the backcross design. In the neighborhood of θ = .5,
the backcross design and the coupling×coupling, double-intercross design
have about equivalent information while the coupling×repulsion, double-
intercross design is of no practical value. In general, if one design has α
times as much information per offspring as a second design, then it takes α
times as many offspring for the second design to achieve the same precision
in estimating θ as the first design.

3.5 Quasi-Newton Methods

Quasi-Newton methods of maximum likelihood update the current ap-
2
proximation A n to the observed information −d L(θ n ) by a low-rank per-