Page 83 - Applied Process Design For Chemical And Petrochemical Plants Volume II

72 Applied Process Design for Chemical and Petrochemical Plants

3. Determine Underwood’s 8 value as previously centrations that were used in or calculated by the Fenske
described, using the average a value. equation for the Underwood solution. (8 = Underwood
4. Calculate (L/D)min and compare with assumed value constant.)
of (1) above. If check is satisfactory, (L/D)min is com-
plete; if not, reassume new (L/D)mh using calculated Underwood Algebraic Method Split Key Systems:
value as basis, and repeat (1) through (4) until satis- Constant Volatility 1721
factory check is obtained.
Although this method appears tedious, it is not so
where to = overhead temp “F unwieldy as to be impractical. It does require close atten-
tB = bottoms temp OF tion to detail. However, a value of (L/D)min can be
t..p = avg temp, “F obtained with one trial that may be satisfactory for “order
of magnitude” use, which is quite often what is desired
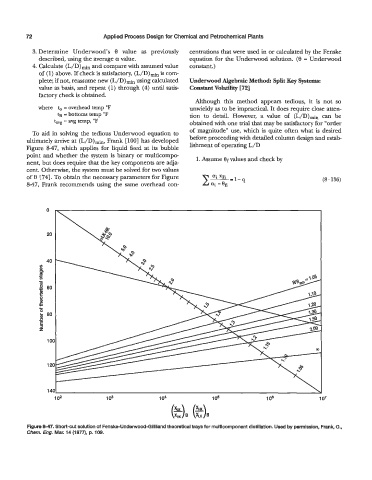
To aid in solving the tedious Underwood equation to
ultimately arrive at (L/D)min, Frank [ 1001 has developed before proceeding with detailed column design and estab-
Figure 8-47’, which applies for liquid feed at its bubble lishment of operating L/D
point and whether the system is binary or multicompe 1. Assume ef values and check by
nent, but does require that the key components are adja-
cent. Otherwise, the system must be solved for two values
of 8 [ 7’41. To obtain the necessary parameters for Figure (8 136)
-
8-47, Frank recommends using the same overhead con-

102 103 1 04 1 05 106 107

Figure 8-47. Short-cut solution of Fenske-Underwood-Gilliland theoretical trays for multicomponent distillation. Used by permission, Frank, O.,
Chem. Eng. Mar. 14 (1973, p. 109.