Page 101 - Applied Statistics And Probability For Engineers

PQ220 6234F.Ch 03 13/04/2002 03:19 PM Page 79

3-7 GEOMETRIC AND NEGATIVE BINOMIAL DISTRIBUTIONS 79

1.0
p
0.1
0.9
0.8

0.6

f (x)
0.4

0.2

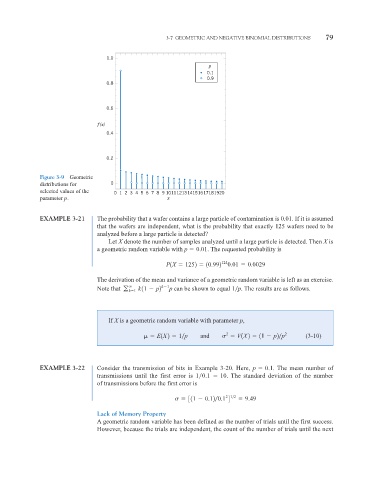
Figure 3-9 Geometric
distributions for 0
selected values of the 0123 4 567 8 9 1011121314151617181920
parameter p. x

EXAMPLE 3-21 The probability that a wafer contains a large particle of contamination is 0.01. If it is assumed
that the wafers are independent, what is the probability that exactly 125 wafers need to be
analyzed before a large particle is detected?
Let X denote the number of samples analyzed until a large particle is detected. Then X is
a geometric random variable with p 0.01. The requested probability is

124
P1X 1252 10.992 0.01 0.0029
The derivation of the mean and variance of a geometric random variable is left as an exercise.
Note that g
k11 p2 k 1 p can be shown to equal 1 p . The results are as follows.
k 1

If X is a geometric random variable with parameter p,

2
E1X2 1 p and V1X2 11 p2 p 2 (3-10)

EXAMPLE 3-22 Consider the transmission of bits in Example 3-20. Here, p 0.1. The mean number of
transmissions until the first error is 1 0.1 10. The standard deviation of the number
of transmissions before the first error is

2 1 2
311 0.12 0.1 4 9.49
Lack of Memory Property
A geometric random variable has been defined as the number of trials until the first success.
However, because the trials are independent, the count of the number of trials until the next