Page 123 - Applied Statistics And Probability For Engineers

c04.qxd 5/10/02 5:19 PM Page 101 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

4-2 PROBABILITY DISTRIBUTIONS AND PROBABILITY DENSITY FUNCTIONS 101

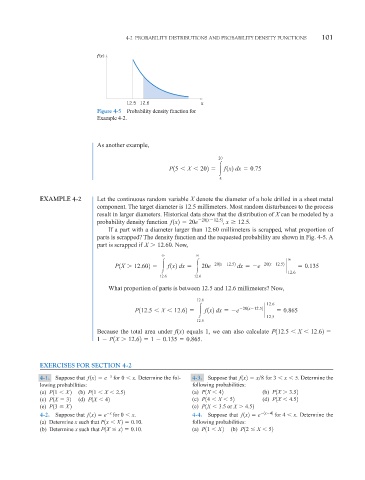
f(x)

12.5 12.6 x
Figure 4-5 Probability density function for
Example 4-2.

As another example,

20

P15 X 202 f 1x2 dx 0.75

5

EXAMPLE 4-2 Let the continuous random variable X denote the diameter of a hole drilled in a sheet metal
component. The target diameter is 12.5 millimeters. Most random disturbances to the process
result in larger diameters. Historical data show that the distribution of X can be modeled by a
probability density function f 1x2 20e 201x 12.52 , x 12.5.
If a part with a diameter larger than 12.60 millimeters is scrapped, what proportion of
parts is scrapped? The density function and the requested probability are shown in Fig. 4-5. A
part is scrapped if X 12.60. Now,

201x 12.52 201x 12.52
P1X 12.602 f 1x2 dx 20e dx e ` 0.135
12.6
12.6 12.6
What proportion of parts is between 12.5 and 12.6 millimeters? Now,

12.6 12.6
201x 12.52
P112.5 X 12.62 f 1x2 dx e ` 0.865
12.5
12.5
Because the total area under f(x) equals 1, we can also calculate P112.5 X 12.62
1 P1X 12.62 1 0.135 0.865.

EXERCISES FOR SECTION 4-2
4-1. Suppose that f 1x2 e x for 0 x. Determine the fol- 4-3. Suppose that f 1x2 x 8 for 3 x 5. Determine the
lowing probabilities: following probabilities:
(a) P11 X 2 (b) P11 X 2.52 (a) P1X 42 (b) P1X 3.52
(c) P1X 32 (d) P1X 42 (c) P14 X 52 (d) P1X 4.52
(e) P13 X 2 (e) P1X 3.5 or X 4.52
4-2. Suppose that f 1x2 e x for 0 x. 4-4. Suppose that f 1x2 e 1x 42 for 4 x. Determine the
(a) Determine x such that P1x X 2 0.10. following probabilities:
(b) Determine x such that P1X x2 0.10. (a) P11 X 2 (b) P12 X 52