Page 125 - Applied Statistics And Probability For Engineers

c04.qxd 5/10/02 5:19 PM Page 103 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

4-3 CUMULATIVE DISTRIBUTION FUNCTIONS 103

and
x

F1x2 f 1u2 du 0.05x, for 0 x 20

0
Finally,
x

F1x2 f 1u2 du 1, for 20 x

0
Therefore,

0 x 0
F1x2 •0.05x 0 x 20
1 20 x

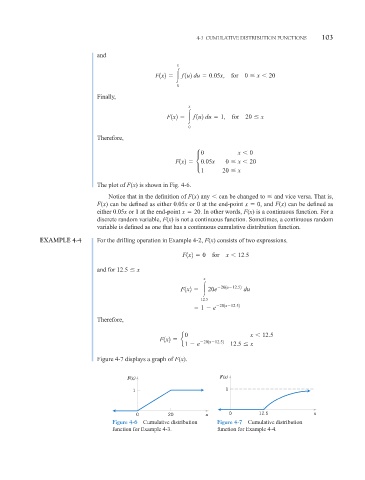
The plot of F(x) is shown in Fig. 4-6.
Notice that in the definition of F(x) any can be changed to and vice versa. That is,
F(x) can be defined as either 0.05x or 0 at the end-point x 0, and F(x) can be defined as
either 0.05x or 1 at the end-point x 20. In other words, F(x) is a continuous function. For a
discrete random variable, F(x) is not a continuous function. Sometimes, a continuous random
variable is defined as one that has a continuous cumulative distribution function.

EXAMPLE 4-4 For the drilling operation in Example 4-2, F(x) consists of two expressions.

F1x2 0 for x 12.5

and for 12.5 x
x

F1x2 20e 201u 12.52 du
12.5
1 e 201x 12.52

Therefore,

0 x 12.5
F1x2 e 201x 12.52
1 e 12.5 x
Figure 4-7 displays a graph of F(x).

F(x) F(x)

1 1

0 20 x 0 12.5 x
Figure 4-6 Cumulative distribution Figure 4-7 Cumulative distribution
function for Example 4-3. function for Example 4-4.