Page 146 - Applied Statistics And Probability For Engineers

c04.qxd 5/10/02 5:20 PM Page 124 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

124 CHAPTER 4 CONTINUOUS RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS

2.0
λ
2
0.5
1.6
0.1

1.2
f(x)

0.8
f (x)

0.4

0.0
0 2 4 6 8 10 12
x 0.1 x
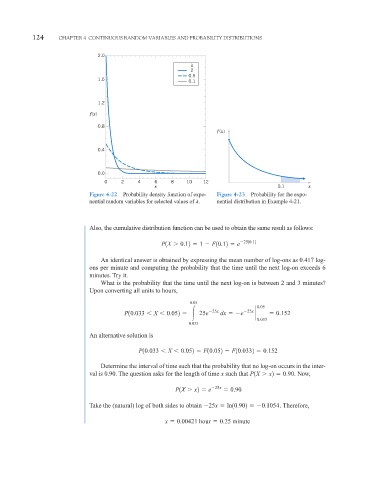
Figure 4-22 Probability density function of expo- Figure 4-23 Probability for the expo-
nential random variables for selected values of . nential distribution in Example 4-21.

Also, the cumulative distribution function can be used to obtain the same result as follows:

P1X 0.12 1 F10.12 e 2510.12

An identical answer is obtained by expressing the mean number of log-ons as 0.417 log-
ons per minute and computing the probability that the time until the next log-on exceeds 6
minutes. Try it.
What is the probability that the time until the next log-on is between 2 and 3 minutes?
Upon converting all units to hours,

0.05 0.05
25x 25x
P10.033 X 0.052 25e dx e ` 0.152
0.033
0.033
An alternative solution is

P10.033 X 0.052 F10.052 F10.0332 0.152

Determine the interval of time such that the probability that no log-on occurs in the inter-
val is 0.90. The question asks for the length of time x such that P1X x2 0.90 . Now,

P1X x2 e 25x 0.90

Take the (natural) log of both sides to obtain 25x ln10.902 0.1054 . Therefore,

x 0.00421 hour 0.25 minute