Page 142 - Applied Statistics And Probability For Engineers

c04.qxd 5/10/02 5:19 PM Page 120 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

120 CHAPTER 4 CONTINUOUS RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS

EXAMPLE 4-18 The digital communication problem in the previous example is solved as follows:

X 160 150 160
P1X 1502 P a b
5
5
216011 10 2 216011 10 2
P1Z 0.792 P1Z 0.792 0.785
6
5
Because np 116 10 211 10 2 160 and n(1 p) is much larger, the approximation
is expected to work well in this case.

EXAMPLE 4-19 Again consider the transmission of bits in Example 4-18. To judge how well the normal
approximation works, assume only n 50 bits are to be transmitted and that the probability
of an error is p 0.1. The exact probability that 2 or less errors occur is

50 50 50 49 50 2 48
P1X 22 a b 0.9
a b 0.110.9 2
a b 0.1 10.9 2 0.112
0 1 2

Based on the normal approximation

X 5 2 5
P1X 22 P a b P1Z 1.422 0.08
2.12 2.12

Even for a sample as small as 50 bits, the normal approximation is reasonable.

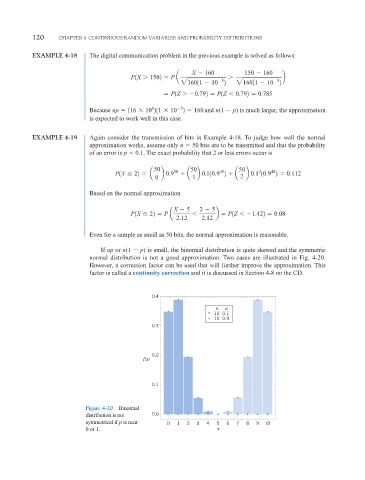
If np or n(1 p) is small, the binomial distribution is quite skewed and the symmetric
normal distribution is not a good approximation. Two cases are illustrated in Fig. 4-20.
However, a correction factor can be used that will further improve the approximation. This
factor is called a continuity correction and it is discussed in Section 4-8 on the CD.

0.4
n p
10 0.1
10 0.9
0.3

0.2
f(x)

0.1

Figure 4-20 Binomial
distribution is not 0.0
symmetrical if p is near 0 1 2 3 4 5 6 7 8 9 10
0 or 1. x