Page 156 - Applied Statistics And Probability For Engineers

c04.qxd 5/13/02 11:19 M Page 134 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

134 CHAPTER 4 CONTINUOUS RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS

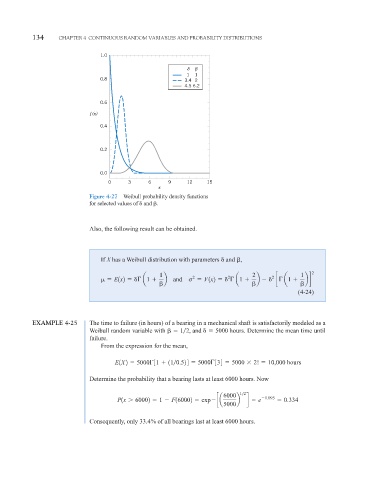
1.0
δ β
1 1
0.8 3.4 2
4.5 6.2

0.6
f (x)

0.4

0.2

0.0
0 3 6 9 12 15
x
Figure 4-27 Weibull probability density functions

for selected values of and .

Also, the following result can be obtained.

If X has a Weibull distribution with parameters and ,

1 2 1 2
2
2
E1x2 a1
b and V 1x2 a1
b c a1
bd
2

(4-24)
EXAMPLE 4-25 The time to failure (in hours) of a bearing in a mechanical shaft is satisfactorily modeled as a
Weibull random variable with 1 2, and 5000 hours. Determine the mean time until
failure.
From the expression for the mean,

E1X2 5000 31
11 0.524 5000 334 5000 2! 10,000 hours

Determine the probability that a bearing lasts at least 6000 hours. Now

6000 1 2 1.095
P1x 60002 1 F160002 exp ca b d e 0.334
5000

Consequently, only 33.4% of all bearings last at least 6000 hours.