Page 303 - Applied Statistics And Probability For Engineers

c08.qxd 5/15/02 6:13 PM Page 255 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark Files:

8-2 CONFIDENCE INTERVAL ON THE MEAN OF A NORMAL DISTRIBUTION, VARIANCE KNOWN 255

The summary statistics from Minitab are displayed below:

Descriptive Statistics: Concentration
Variable N Mean Median TrMean StDev SE Mean
Concentration 53 0.5250 0.4900 0.5094 0.3486 0.0479
Variable Minimum Maximum Q1 Q3
Concentration 0.0400 1.3300 0.2300 0.7900

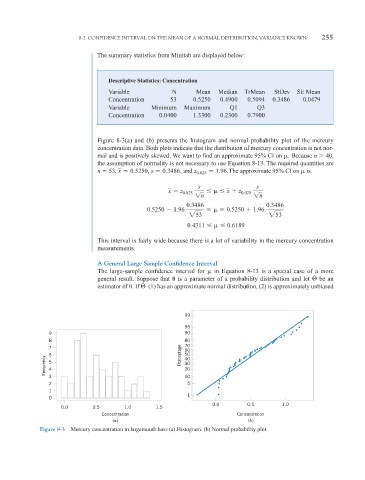
Figure 8-3(a) and (b) presents the histogram and normal probability plot of the mercury
concentration data. Both plots indicate that the distribution of mercury concentration is not nor-
mal and is positively skewed. We want to find an approximate 95% CI on . Because n
40,
the assumption of normality is not necessary to use Equation 8-13. The required quantities are
n 53, x 0.5250, s 0.3486 , and z 0.025 1.96. The approximate 95% CI on is

s s
x z 0.025 x z 0.025
1n 1n
0.3486 0.3486
0.5250 1.96 0.5250 1.96
253 253
0.4311 0.6189

This interval is fairly wide because there is a lot of variability in the mercury concentration
measurements.

A General Large Sample Confidence Interval
The large-sample confidence interval for in Equation 8-13 is a special case of a more
ˆ
general result. Suppose that is a parameter of a probability distribution and let be an
ˆ
estimator of . If (1) has an approximate normal distribution, (2) is approximately unbiased

99
95
9 90
8 80
7 70
60
6 Percentage 50
Frequency 5 30
40
20
4
3 10
2 5
1
1
0
0.0 0.5 1.0
0.0 0.5 1.0 1.5
Concentration Concentration
(a) (b)
Figure 8-3 Mercury concentration in largemouth bass (a) Histogram. (b) Normal probability plot.