Page 326 - Applied Statistics And Probability For Engineers

PQ220 6234F.CD(08) 5/15/02 6:38 PM Page 2 RK UL 6 RK UL 6:Desktop Folder:TEMP WORK:MONTGOMERY:REVISES UPLO D CH114 FIN L:Quark F

8-2

80 100

80
60
Frequency 40 Frequency 60

40
20
20

0 0
0 0.03 0.06 0.09 0.12 0.15 0.18 _ 0.04 0 0.04 0.08 0.12
^ * _
λ i λ i λ *
^
(a) Histogram of the bootstrap estimate (b) Histogram of the differences λ i * _ λ *
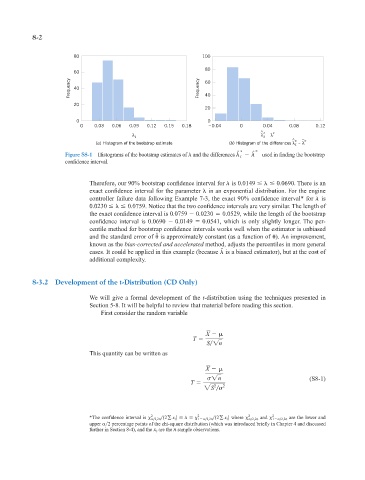
Figure S8-1 Histograms of the bootstrap estimates of and the differences ˆ * i ˆ * used in finding the bootstrap
confidence interval.

Therefore, our 90% bootstrap confidence interval for is 0.0149

0.0690. There is an
exact confidence interval for the parameter in an exponential distribution. For the engine
controller failure data following Example 7-3, the exact 90% confidence interval* for is
0.0230

0.0759. Notice that the two confidence intervals are very similar. The length of
the exact confidence interval is 0.0759 0.0230 0.0529, while the length of the bootstrap
confidence interval is 0.0690 0.0149 0.0541, which is only slightly longer. The per-
centile method for bootstrap confidence intervals works well when the estimator is unbiased
ˆ
and the standard error of is approximately constant (as a function of ). An improvement,

known as the bias-corrected and accelerated method, adjusts the percentiles in more general
ˆ
cases. It could be applied in this example (because is a biased estimator), but at the cost of

additional complexity.
8-3.2 Development of the t-Distribution (CD Only)

We will give a formal development of the t-distribution using the techniques presented in
Section 5-8. It will be helpful to review that material before reading this section.
First consider the random variable

X
T
S 1n
This quantity can be written as

X
1 n (S8-1)
T
2
2S 2

2
2
2
2
*The confidence interval is 2,2n 12g x i 2

1 2,2n 12g x i 2 where 2,2n and 1 2,2n are the lower and
upper 2 percentage points of the chi-square distribution (which was introduced briefly in Chapter 4 and discussed
n
further in Section 8-4), and the x i are the sample observations.