Page 333 - Applied Statistics And Probability For Engineers

c09.qxd 5/15/02 8:02 PM Page 281 RK UL 9 RK UL 9:Desktop Folder:

9-1 HYPOTHESIS TESTING 281

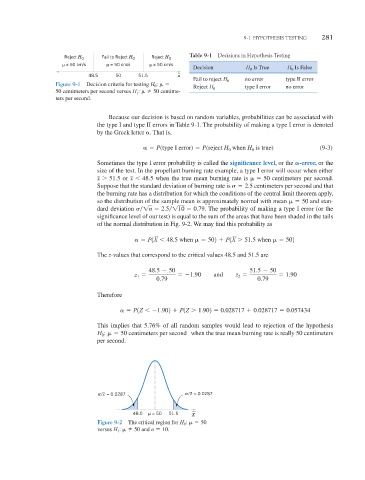
Table 9-1 Decisions in Hypothesis Testing
Fail to Reject H Reject H
Reject H 0 0 0
µ ≠ 50 cm/s µ = 50 cm/s µ ≠ 50 cm/s
Decision H 0 Is True H 0 Is False
48.5 50 51.5 x
Fail to reject H 0 no error type II error
Figure 9-1 Decision criteria for testing H 0 :
Reject H 0 type I error no error
50 centimeters per second versus H 1 : 50 centime-
ters per second.
Because our decision is based on random variables, probabilities can be associated with
the type I and type II errors in Table 9-1. The probability of making a type I error is denoted
by the Greek letter . That is,

P(type I error) P(reject H when H is true) (9-3)
0
0
Sometimes the type I error probability is called the significance level, or the -error, or the
size of the test. In the propellant burning rate example, a type I error will occur when either
x 51.5 or x 48.5 when the true mean burning rate is 50 centimeters per second.
Suppose that the standard deviation of burning rate is 2.5 centimeters per second and that
the burning rate has a distribution for which the conditions of the central limit theorem apply,
so the distribution of the sample mean is approximately normal with mean 50 and stan-
dard deviation
1n 2.5
110 0.79 . The probability of making a type I error (or the
significance level of our test) is equal to the sum of the areas that have been shaded in the tails
of the normal distribution in Fig. 9-2. We may find this probability as

P1X 48.5 when 502 P1X 51.5 when 502

The z-values that correspond to the critical values 48.5 and 51.5 are

48.5
50 51.5
50
z 1
1.90 and z 2 1.90
0.79 0.79

Therefore

P1Z
1.902 P1Z 1.902 0.028717 0.028717 0.057434

This implies that 5.76% of all random samples would lead to rejection of the hypothesis
H 0 : 50 centimeters per second when the true mean burning rate is really 50 centimeters
per second.

α /2 = 0.0287 α /2 = 0.0287

48.5 µ = 50 51.5 X
Figure 9-2 The critical region for H 0 : 50
versus H 1 : 50 and n 10.