Page 335 - Applied Statistics And Probability For Engineers

c09.qxd 5/15/02 8:02 PM Page 283 RK UL 9 RK UL 9:Desktop Folder:

9-1 HYPOTHESIS TESTING 283

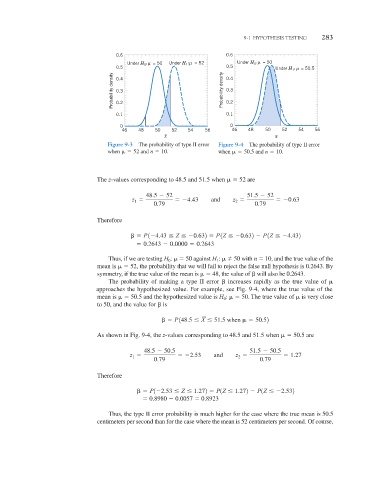
0.6 0.6
µ
µ
µ
Under H 0 : = 50 Under H 1 : = 52 Under H 0 : = 50
µ
0.5 0.5 Under H 1 : = 50.5
Probability density 0.3 Probability density 0.3
0.4
0.4
0.2
0.2
0.1 0.1
0 0
46 48 50 52 54 56 46 48 50 52 54 56
– –
x x
Figure 9-3 The probability of type II error Figure 9-4 The probability of type II error
when 52 and n 10. when 50.5 and n 10.

The z-values corresponding to 48.5 and 51.5 when 52 are

48.5
52 51.5
52
z
4.43 and z
0.63
2
1
0.79 0.79
Therefore

P1
4.43 Z
0.632 P1Z
0.632
P1Z
4.432
0.2643
0.0000 0.2643

Thus, if we are testing H : 50 against H : 50 with n 10, and the true value of the
1
0
mean is 52, the probability that we will fail to reject the false null hypothesis is 0.2643. By
symmetry, if the true value of the mean is 48, the value of will also be 0.2643.
The probability of making a type II error increases rapidly as the true value of
approaches the hypothesized value. For example, see Fig. 9-4, where the true value of the
mean is 50.5 and the hypothesized value is H : 50. The true value of is very close
0
to 50, and the value for is

P148.5 X 51.5 when 50.52

As shown in Fig. 9-4, the z-values corresponding to 48.5 and 51.5 when 50.5 are

48.5
50.5 51.5
50.5
z
2.53 and z 1.27
1
2
0.79 0.79
Therefore

P1
2.53 Z 1.272 P1Z 1.272
P1Z
2.532
0.8980
0.0057 0.8923

Thus, the type II error probability is much higher for the case where the true mean is 50.5
centimeters per second than for the case where the mean is 52 centimeters per second. Of course,