Page 49 - Artificial Intelligence for the Internet of Everything

36 Artificial Intelligence for the Internet of Everything

calculation of these M-H ratios necessitates a pass through the entire dataset,
scalability of HMC-based algorithms has been limited. This has been
addressed recently with the development of stochastic approaches, inspired
by the now ubiquitous SGD-based ERM algorithms, where we omit the
M-H correction step and calculate the Hamiltonian gradients over random
mini-batches of the training data (Chen, Fox, & Guestrin, 2014; Welling &
Teh, 2011). Further improvements to these approaches have been done by
incorporating Riemann manifold techniques to learn the critically important
Hamiltonian mass matrices, both in the standard HMC (Girolami & Calder-
head, 2011) and stochastic (Ma, Chen, & Fox, 2015; Roychowdhury,
Kulis, & Parthasarathy, 2016) settings. These Riemannian approaches have
been shown to noticeably improve the acceptance probabilities of samples
following the methods of those proposed by Girolami and Calderhead
(2011), and dramatically improve the convergence rates in the stochastic
formulations as well (Roychowdhury et al., 2016).
Preliminary experiments show that HMC does not work well in prac-
tice. Thus one can identify two challenges with posterior sampling using
HMC. First, HMC still has a hard time finding the different modes of the
distribution (i.e., if it can escape metastable regions of the HMC Markov
chain). Second, as stated earlier, the massive dimensionality of deep neural
networks make the most of the posterior probability mass that resides in
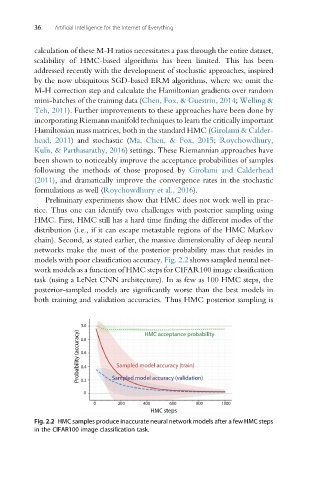
models with poor classification accuracy. Fig. 2.2 shows sampled neural net-
work models as a function of HMC steps for CIFAR100 image classification
task (using a LeNet CNN architecture). In as few as 100 HMC steps, the
posterior-sampled models are significantly worse than the best models in
both training and validation accuracies. Thus HMC posterior sampling is

Fig. 2.2 HMC samples produce inaccurate neural network models after a few HMC steps
in the CIFAR100 image classification task.