Page 237 - Autonomous Mobile Robots

222 Autonomous Mobile Robots

(a) 1 (b) 1
x
y
0.5
u 0.5
0
y 0
– 0.5
– 0.5
– 1
– 1.5 1
0 10 20 30 40 – 1 – 0.5 0 0.5 1
t (sec) x
(c) 10 (d) 5
u 1T
4
u 2T
5
3
log(V T )
0 2
1
– 5
0
– 10 – 1
0 10 20 30 40 0 10 20 30 40
t (sec) t (sec)
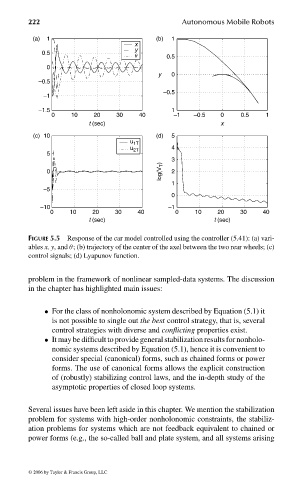
FIGURE 5.5 Response of the car model controlled using the controller (5.41): (a) vari-
ables x, y, and θ; (b) trajectory of the center of the axel between the two rear wheels; (c)
control signals; (d) Lyapunov function.

problem in the framework of nonlinear sampled-data systems. The discussion
in the chapter has highlighted main issues:

• For the class of nonholonomic system described by Equation (5.1) it
is not possible to single out the best control strategy, that is, several
control strategies with diverse and conflicting properties exist.
• It may be difficult to provide general stabilization results for nonholo-
nomic systems described by Equation (5.1), hence it is convenient to
consider special (canonical) forms, such as chained forms or power
forms. The use of canonical forms allows the explicit construction
of (robustly) stabilizing control laws, and the in-depth study of the
asymptotic properties of closed loop systems.

Several issues have been left aside in this chapter. We mention the stabilization
problem for systems with high-order nonholonomic constraints, the stabiliz-
ation problems for systems which are not feedback equivalent to chained or
power forms (e.g., the so-called ball and plate system, and all systems arising

© 2006 by Taylor & Francis Group, LLC

FRANKL: “dk6033_c005” — 2006/3/31 — 16:42 — page 222 — #36