Page 304 - Becoming Metric Wise

296 Becoming Metric-Wise

k 5 ln(a). We further note that an exponential function may not be con-
b
fused with a power function, which is a function of the form t (with t
the variable and b a constant).
In the previous example we assumed that a(t) is a constant. This
assumption does not always hold, of course, as a synchronous citation
curve often has the form shown in Fig. 6.1. Citation curves can be
described approximately as a fast increasing function, followed by a
decreasing function which can—from a certain point on be approximated
by an exponential function. In the informetric literature, such citation
curves have been described by lognormal functions, see Matricciani
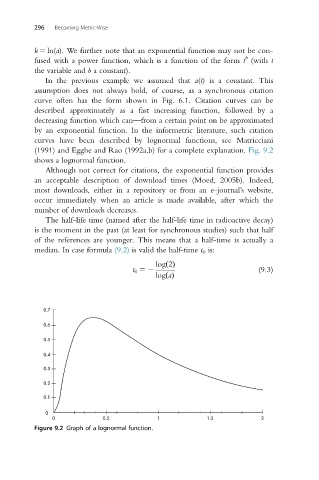
(1991) and Egghe and Rao (1992a,b) for a complete explanation. Fig. 9.2
shows a lognormal function.
Although not correct for citations, the exponential function provides
an acceptable description of download times (Moed, 2005b). Indeed,
most downloads, either in a repository or from an e-journal’s website,
occur immediately when an article is made available, after which the
number of downloads decreases.
The half-life time (named after the half-life time in radioactive decay)
is the moment in the past (at least for synchronous studies) such that half
of the references are younger. This means that a half-time is actually a
median. In case formula (9.2) is valid the half-time t 0 is:
log 2ðÞ
t 0 52 (9.3)
log aðÞ

Figure 9.2 Graph of a lognormal function.